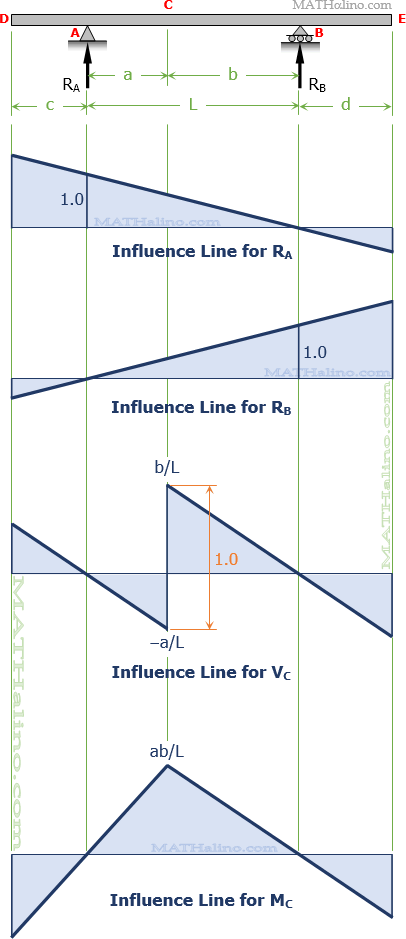
Influence Lines for Beams
A downward concentrated load of magnitude 1 unit moves from A to B across the simply supported beam AB as shown below.
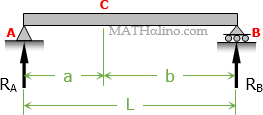
We wish to determine the following functions:
- reaction at A
- reaction at B
- shear at C and
- moment at C
when the unit load is at a distance x from support A. Since the value of the above functions will vary according to the location of the unit load, the best way to represent these functions is by influence diagram.
Influence Line by Equilibrium Method
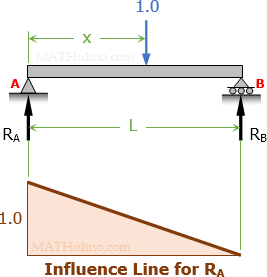
Influence Line for the reaction at A
$LR_A = 1.0(L - x)$
$R_A = 1 - \dfrac{x}{L}$ ← linear equation in x
When x = 0, RA = 1 and when x = L, RA = 0
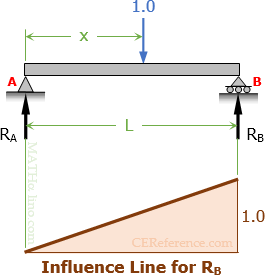
Influence Line for the reaction at B
$LR_B = 1.0x$
$R_B = \dfrac{x}{L}$ ← linear equation in x
When x = 0, RB = 0, and when x = L, RB = 1
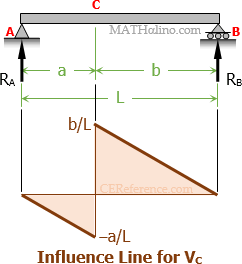
Influence Line for Shear at C
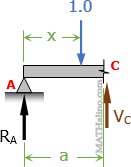Unit load is within the segment AC$V_C = R_A - 1.0$
$V_C = \left( 1 - \dfrac{x}{L} \right) - 1.0$
$V_C = -\dfrac{x}{L}$
When x = 0, VC = 0, and when x = a (just before point C), VC = -a/L
Unit load is beyond the segment AC
$V_C = R_A$
$V_C = 1 - \dfrac{x}{L}$
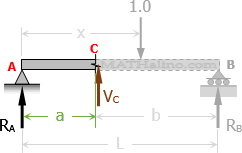
When x = a (just after point C), VC = 1 - a/L = (L - a) / L = b/L and when x = L, VC = 1 - L/L = 0
Influence Line for Moment at C
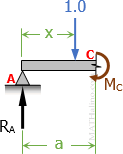Unit load is within the segment AC$M_C = aR_A - 1.0(a - x)$
$M_C = a\left( 1 - \dfrac{x}{L} \right) - (a - x)$
$M_C = a - \dfrac{ax}{L} - a + x$
$M_C = -\dfrac{ax}{L} + x$
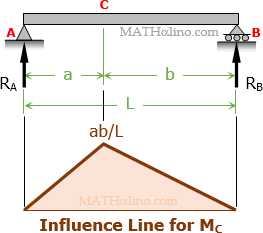
When x = 0, MC = 0, and when x = a (just just before point C), MC = -a2/L + a = (-a2 + aL) / L = a(L - a) / L = ab/L
Unit load is beyond the segment AC
$M_C = aR_A = a\left( 1 - \dfrac{x}{L} \right)$
$M_C = a - \dfrac{ax}{L}$
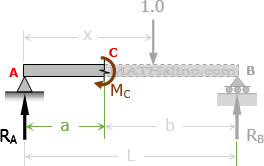
When x = a (just after point C), MC = a - a2/L = (aL - a2) / L = a(L - a) / L = ab/L and when x = L, MC = a - aL/L = a - a = 0
Influence Line of Simply Supported Beam with Overhang
The ordinate of influence line at the overhang can be found by ratio and proportion of triangle.
