Derivation of Formula for Volume of the Sphere by Integration
For detailed information about sphere, see the Solid Geometry entry, The Sphere.
The formula for the volume of the sphere is given by
Solution to Problem 696-697 | Beam Deflection by Method of Superposition
Problem 696
In Fig. P-696, determine the value of P for which the deflection under P will be zero.
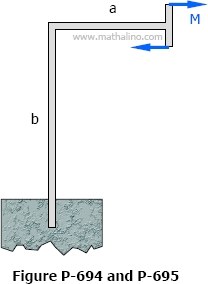
Solution to Problem 694-695 | Beam Deflection by Method of Superposition
Problem 694
The frame shown in Fig. P-694 is of constant cross section and is perfectly restrained at its lower end. Compute the vertical deflection caused by the couple M.
Solution to Problem 693 | Beam Deflection by Method of Superposition
Problem 693
Determine the value of EIδ at the left end of the overhanging beam in Fig. P-693.
Solution to Problem 692 | Beam Deflection by Method of Superposition
Problem 692
Find the value of EIδ midway between the supports for the beam shown in Fig. P-692. (Hint: Combine Case No. 11 and one half of Case No. 8.)
Solution to Problem 691 | Beam Deflection by Method of Superposition
Problem 691
Determine the midspan deflection for the beam shown in Fig. P-691. (Hint: Apply Case No. 7 and integrate.)
Solution to Problem 689 | Beam Deflection by Method of Superposition
Problem 689
The beam shown in Fig. P-689 has a rectangular cross section 4 inches wide by 8 inches deep. Compute the value of P that will limit the midspan deflection to 0.5 inch. Use E = 1.5 × 106 psi.
Solution to Problem 688 | Beam Deflection by Method of Superposition
Problem 688
Determine the midspan value of EIδ at the left end of the beam shown in Fig. P-688.
Solution to Problem 687 | Beam Deflection by Method of Superposition
Problem 687
Determine the midspan deflection of the beam shown in Fig. P-687 if E = 10 GPa and I = 20 × 106 mm4.

Recent comments