Problem
Evaluate $\displaystyle \int \left( \sqrt{x} + x\sqrt{x} + \dfrac{1}{\sqrt{x}} \right) \, dx$
 

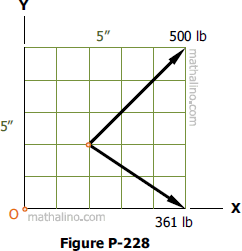
Problem 228
Without computing the magnitude of the resultant, compute where the resultant of the forces shown in Fig. P-228 intersects the x and y axes.
 

Problem 227
Two forces P and Q pass through a point A which is 4 m to the right of and 3 m above a moment center O. Force P is 890 N directed up to the right at 30° with the horizontal and force Q is 445 N directed up to the left at 60° with the horizontal. Determine the moment of the resultant of these two forces with respect to O.
 

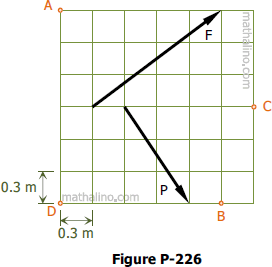
Problem 226
In Fig. P-226 assuming counterclockwise moments as positive, compute the moment of force F = 200 kg and force P = 165 kg about points A, B, C, and D.
 

Moment is the measure of the capacity or ability of the force to produce twisting or turning effect about an axis. This axis is perpendicular to the plane containing the line of action of the force. The magnitude of moment is equal to the product of the force and the perpendicular distance from the axis to the line of action of the force. The intersection of the plane and the axis is commonly called the moment center, and the perpendicular distance from the moment center to the line of action of the force is called moment arm.
 

Definition of Parabola

Parabola is the locus of point that moves such that it is always equidistant from a fixed point and a fixed line. The fixed point is called focus and the fixed line is called directrix.
 

Definition

Hyperbola can be defined as the locus of point that moves such that the difference of its distances from two fixed points called the foci is constant. The constant difference is the length of the transverse axis, 2a.
 

Elements of the ellipse are shown in the figure below.
 

Definition of Ellipse
Ellipse is the locus of point that moves such that the sum of its distances from two fixed points called the foci is constant. The constant sum is the length of the major axis, 2a.
 

Definition
Conic sections can be defined as the locus of point that moves so that the ratio of its distance from a fixed point called the focus to its distance from a fixed line called the directrix is constant. The constant ratio is called the eccentricity of the conic.