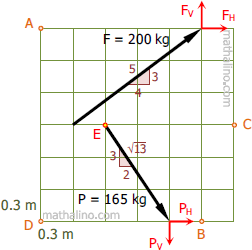
$F_H = F(\frac{4}{5}) = 200(\frac{4}{5})$
$F_H = 160 \, \text{ kg}$
$F_V = F(\frac{3}{5}) = 200(\frac{3}{5})$
$F_V = 120 \, \text{ kg}$
$P_H = P(\frac{2}{\sqrt{13}}) = 165(\frac{2}{\sqrt{13}})$
$P_H = 91.526 \, \text{ kg}$
$P_V = P(\frac{3}{\sqrt{13}}) = 165(\frac{3}{\sqrt{13}})$
$P_V = 137.288 \, \text{ kg}$
Moment of force F about points A, B, C, and D:
$M_A = 5(0.3)F_V = 5(0.3)(120)$
$M_A = 180 \, \text{ kg}\cdot \text{m}$ → answer
$M_B = -6(0.3)F_H = -6(0.3)(160)$
$M_B = -288 \, \text{ kg}\cdot \text{m}$ → answer
$M_C = -0.3F_V - 3(0.3)F_H = -0.3(120) - 3(0.3)(160)$
$M_C = -180 \, \text{ kg}\cdot \text{m}$ → answer
$M_D = 5(0.3)F_V - 6(0.3)F_H = 5(0.3)(120) - 6(0.3)(160)$
$M_C = -108 \, \text{ kg}\cdot \text{m}$ → answer
Moment of force P about points A, B, C, and D:
$M_A = 6(0.3)P_H - 4(0.3)P_V = 6(0.3)(91.526) - 4(0.3)(137.288)$
$M_A = 0$ (this means that point A is on the line of action of force P) → answer
$M_B = 0.3P_V = 0.3(137.288)$
$M_B = 41.186 \, \text{ kg}\cdot \text{m}$ → answer
$M_C = 2(0.3)P_V + 3(0.3)P_H = 2(0.3)(137.288) + 3(0.3)(91.526)$
$M_C = 164.746 \, \text{ kg}\cdot \text{m}$ → answer
You can also resolve P to horizontal and vertical components at point E then take the moment of these components at point C. The answer would be the same. Try it.
$M_D = -4(0.3)P_V = -4(0.3)(137.288)$
$M_D = -164.746 \, \text{ kg}\cdot \text{m}$ → answer
