Resultant of Concurrent Force System
Resultant of a force system is a force or a couple that will have the same effect to the body, both in translation and rotation, if all the forces are removed and replaced by the resultant.
The equation involving the resultant of force system are the following
- $R_x = \Sigma F_x = F_{x1} + F_{x2} + F_{x3} + ...$
The x-component of the resultant is equal to the summation of forces in the x-direction. - $R_y = \Sigma F_y = F_{x1} + F_{x2} + F_{x3} + ...$
The y-component of the resultant is equal to the summation of forces in the y-direction. - $R_z = \Sigma F_z = F_{x1} + F_{x2} + F_{x3} + ...$
The z-component of the resultant is equal to the summation of forces in the z-direction.
Note that according to the type of force system, one or two or three of the equations above will be used in finding the resultant.
Resultant of Coplanar Concurrent Force System
The line of action of each forces in coplanar concurrent force system are on the same plane. All of these forces meet at a common point, thus concurrent. In x-y plane, the resultant can be found by the following formulas:
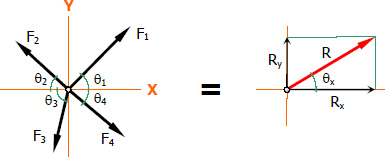
$R_y = \Sigma F_y$
$R = \sqrt{{R_x}^2 + {R_y}^2}$
$\tan \theta_x = \dfrac{R_y}{R_x}$
Resultant of Spatial Concurrent Force System
Spatial concurrent forces (forces in 3-dimensional space) meet at a common point but do not lie in a single plane. The resultant can be found as follows:
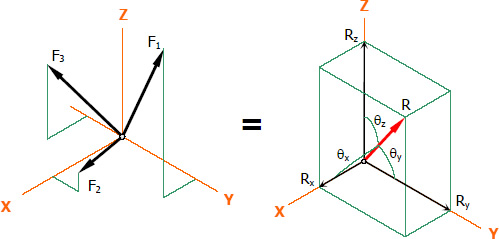
$R_y = \Sigma F_y$
$R_z = \Sigma F_z$
$R = \sqrt{{R_x}^2 + {R_y}^2 + {R_z}^2}$
Direction Cosines
$\cos \theta_y = \dfrac{R_y}{R}$
$\cos \theta_z = \dfrac{R_z}{R}$
Vector Notation of the Resultant
${\bf R} = \Sigma {\bf F}$
${\bf R} = (\Sigma F_x) {\bf i} + (\Sigma F_y) {\bf j} + (\Sigma F_z) {\bf k}$
Where
$R_x = \Sigma F_x$
$R_y = \Sigma F_y$
$R_z = \Sigma F_z$
$R = \sqrt{{R_x}^2 + {R_y}^2 + {R_z}^2}$
- Log in to post comments
