Method of Sections | Analysis of Simple Trusses
Method of Sections
In this method, we will cut the truss into two sections by passing a cutting plane through the members whose internal forces we wish to determine. This method permits us to solve directly any member by analyzing the left or the right section of the cutting plane.
To remain each section in equilibrium, the cut members will be replaced by forces equivalent to the internal load transmitted to the members. Each section may constitute of non-concurrent force system from which three equilibrium equations can be written.
- Read more about Method of Sections | Analysis of Simple Trusses
- Log in or register to post comments
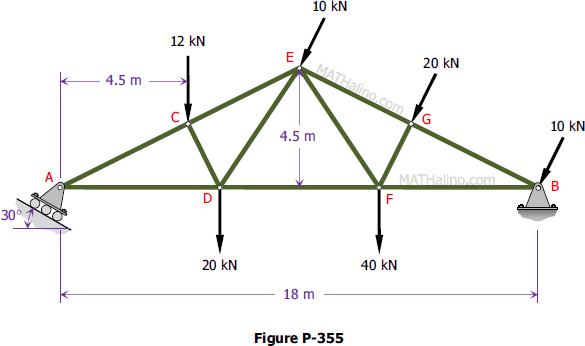
Problem 355 | Equilibrium of Non-Concurrent Force System
Problem 355
Determine the reactions at A and B on the Fink truss shown in Fig. P-355. Members CD and FG are respectively perpendicular to AE and BE at their midpoints.
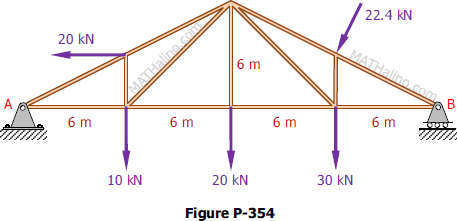
Problem 354 | Equilibrium of Non-Concurrent Force System
Problem 354
Compute the total reactions at A and B on the truss shown in Fig. P-354.
Problem 352 | Equilibrium of Non-Concurrent Force System
Problem 352
A pulley 4 ft in diameter and supporting a load 200 lb is mounted at B on a horizontal beam as shown in Fig. P-352. The beam is supported by a hinge at A and rollers at C. Neglecting the weight of the beam, determine the reactions at A and C.

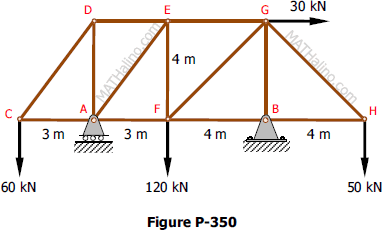
Problem 350 | Equilibrium of Non-Concurrent Force System
Problem 350
Compute the total reactions at A and B for the truss shown in Fig. P-350.
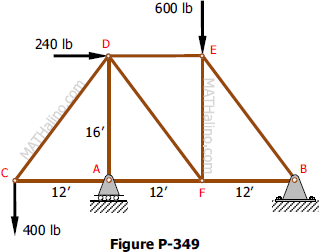
Problem 349 | Equilibrium of Non-Concurrent Force System
Problem 349
The truss shown in Fig. P-349 is supported on roller at A and hinge at B. Solve for the components of the reactions.
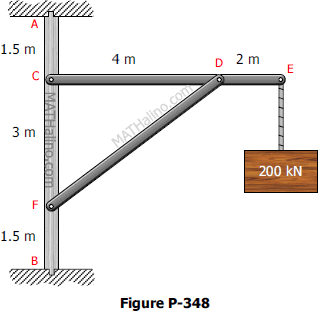
Problem 348 | Equilibrium of Non-Concurrent Force System
Problem 348
The frame shown in Fig. P-348 is supported in pivots at A and B. Each member weighs 5 kN/m. Compute the horizontal reaction at A and the horizontal and vertical components of the reaction at B.
Problem 347 | Equilibrium of Non-Concurrent Force System
Problem 347
Repeat Problem 346 if the cable pulls the boom AB into a position at which it is inclined at 30° above the horizontal. The loads remain vertical.
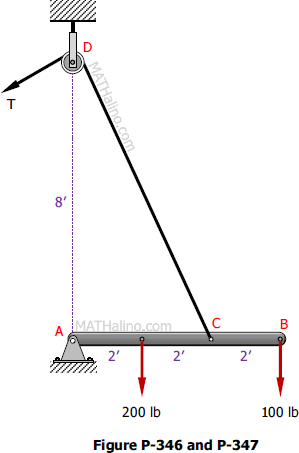
Problem 346 | Equilibrium of Non-Concurrent Force System
Problem 346
A boom AB is supported in a horizontal position by a hinge A and a cable which runs from C over a small pulley at D as shown in Fig. P-346. Compute the tension T in the cable and the horizontal and vertical components of the reaction at A. Neglect the size of the pulley at D.

Equilibrium of Non-Concurrent Force System
There are three equilibrium conditions that can be used for non-concurrent, non-parallel force system.
The sum of all forces in the x-direction or horizontal is zero.
- Read more about Equilibrium of Non-Concurrent Force System
- Log in or register to post comments
