Problem 347 | Equilibrium of Non-Concurrent Force System

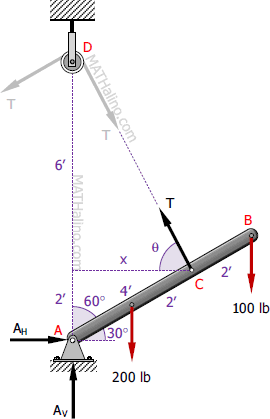
$\sin 60^\circ = \dfrac{x}{4}$

$x = 4 \sin 60^\circ$
 

$\tan \theta = \dfrac{6}{x}$

$\tan \theta = \dfrac{6}{4 \sin 60^\circ}$

$\tan \theta = \sqrt{3}$

$\theta = 60^\circ$
 

Because θ = 60°, T is perpendicular to AB.
$\Sigma M_A = 0$

$4T = 200(2 \cos 30^\circ) + 100(6 \cos 30^\circ)$

$T = 216.51 \, \text{ lb}$           answer
 

$\Sigma F_H = 0$

$A_H = T \cos \theta$

$A_H = 216.51 \cos 60^\circ$

$A_H = 108.25 \, \text{ lb}$           answer
 

$\Sigma F_V = 0$

$A_V + T \sin \theta = 200 + 100$

$A_V + 216.51 \sin 60^\circ = 200 + 100$

$A_V = 112.50 \, \text{ lb}$           answer