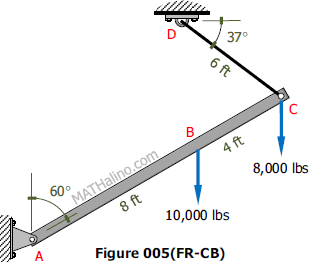
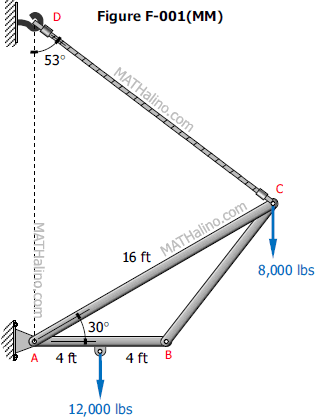
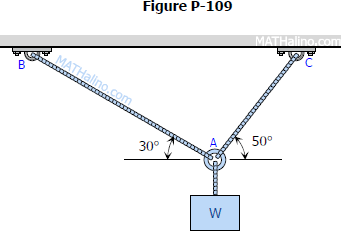
Problem 007-cb | Analysis of Cabled Frame
Problem 007-cb
In the structure shown in Fig. CB-007(FR), members BCE, and CD are assumed to be solid rigid members. Members AE and DE are cables. For this structure, determine the
reaction at B.

- Read more about Problem 007-cb | Analysis of Cabled Frame
- Log in to post comments