non-parallel forces

Problem 355
Determine the reactions at A and B on the Fink truss shown in Fig. P-355. Members CD and FG are respectively perpendicular to AE and BE at their midpoints.
 

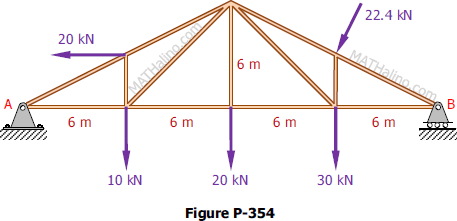
Problem 354
Compute the total reactions at A and B on the truss shown in Fig. P-354.
 

Problem 352
A pulley 4 ft in diameter and supporting a load 200 lb is mounted at B on a horizontal beam as shown in Fig. P-352. The beam is supported by a hinge at A and rollers at C. Neglecting the weight of the beam, determine the reactions at A and C.
 

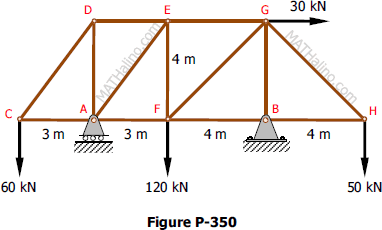
Problem 350
Compute the total reactions at A and B for the truss shown in Fig. P-350.
 

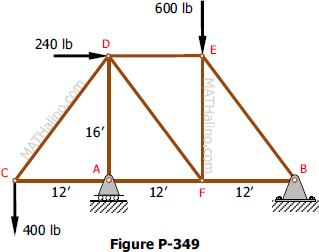
Problem 349
The truss shown in Fig. P-349 is supported on roller at A and hinge at B. Solve for the components of the reactions.
 

Problem 348
The frame shown in Fig. P-348 is supported in pivots at A and B. Each member weighs 5 kN/m. Compute the horizontal reaction at A and the horizontal and vertical components of the reaction at B.
 

Problem 347
Repeat Problem 346 if the cable pulls the boom AB into a position at which it is inclined at 30° above the horizontal. The loads remain vertical.
 

Problem 346
A boom AB is supported in a horizontal position by a hinge A and a cable which runs from C over a small pulley at D as shown in Fig. P-346. Compute the tension T in the cable and the horizontal and vertical components of the reaction at A. Neglect the size of the pulley at D.
 

There are three equilibrium conditions that can be used for non-concurrent, non-parallel force system.
 

The sum of all forces in the x-direction or horizontal is zero.

The resultant of non-concurrent force system is defined according to magnitude, inclination, and position.
 

The magnitude of the resultant can be found as follows