static equilibrium

Problem 361
Referring to Problem 359, if T = 30 kN and x = 1 m, determine the angle θ at which the bar will be inclined to the horizontal when it is in a position of equilibrium.
 

Problem 360
Referring to Problem 359, what value of T acting at x = 1 m from B will keep the bar horizontal.
 

Problem 359
A 4-m bar of negligible weight rests in a horizontal position on the smooth planes shown in Fig. P-359. Compute the distance x at which load T = 10 kN should be placed from point B to keep the bar horizontal.
 

Problem 358
A bar AE is in equilibrium under the action of the five forces shown in Fig. P-358. Determine P, R, and T.
 

Problem 347
Repeat Problem 346 if the cable pulls the boom AB into a position at which it is inclined at 30° above the horizontal. The loads remain vertical.
 

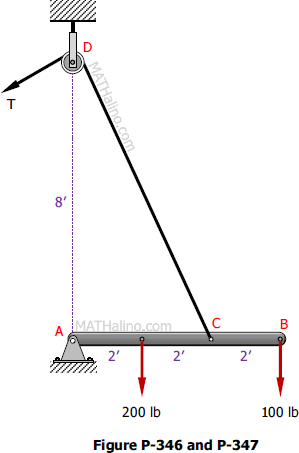
Problem 346
A boom AB is supported in a horizontal position by a hinge A and a cable which runs from C over a small pulley at D as shown in Fig. P-346. Compute the tension T in the cable and the horizontal and vertical components of the reaction at A. Neglect the size of the pulley at D.
 

There are three equilibrium conditions that can be used for non-concurrent, non-parallel force system.
 

The sum of all forces in the x-direction or horizontal is zero.

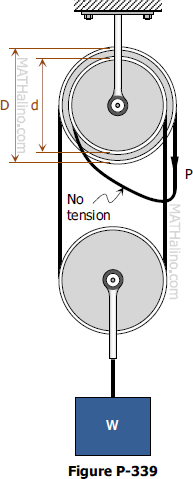
Problem 339
The differential chain hoist shown in Fig. P-339 consists of two concentric pulleys rigidly fastened together. The pulleys form two sprockets for an endless chain looped over them in two loops. In one loop is mounted a movable pulley supporting a load W. Neglecting friction, determine the maximum load W that can just be raised by a pull P supplied as shown.
 

Problem 329
Two cylinders A and B, weighing 100 lb and 200 lb respectively, are connected by a rigid rod curved parallel to the smooth cylindrical surface shown in Fig. P-329. Determine the angles α and β that define the position of equilibrium.