reaction

Problem 348
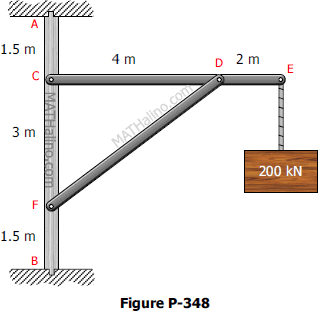
The frame shown in Fig. P-348 is supported in pivots at A and B. Each member weighs 5 kN/m. Compute the horizontal reaction at A and the horizontal and vertical components of the reaction at B.
 

Problem 347
Repeat Problem 346 if the cable pulls the boom AB into a position at which it is inclined at 30° above the horizontal. The loads remain vertical.
 

Problem 346
A boom AB is supported in a horizontal position by a hinge A and a cable which runs from C over a small pulley at D as shown in Fig. P-346. Compute the tension T in the cable and the horizontal and vertical components of the reaction at A. Neglect the size of the pulley at D.
 

Problem 336
The cantilever beam shown in Fig. P-336 is built into a wall 2 ft thick so that it rests against points A and B. The beam is 12 ft long and weighs 100 lb per ft.
 

Problem 326
The cylinders in Fig. P-326 have the indicated weights and dimensions. Assuming smooth contact surfaces, determine the reactions at A, B, C, and D on the cylinders.
 

Problem 244
A homogeneous bar with a cross sectional area of 500 mm² is attached to rigid supports. It carries the axial loads P₁ = 25 kN and P₂ = 50 kN, applied as shown in Fig. P-244. Determine the stress in segment BC. (Hint: Use the results of Prob. 243, and compute the reactions caused by P₁ and P₂ acting separately. Then use the principle of superposition to compute the reactions when both loads are applied.)
 

Problem 243
A homogeneous rod of constant cross section is attached to unyielding supports. It carries an axial load P applied as shown in Fig. P-243. Prove that the reactions are given by R₁ = Pb/L and R₂ = Pa/L.