011 Resultant of three forces acting in a ring

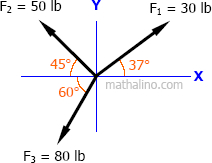
$R_x = \Sigma F_x$

$R_x = 30 \cos 37^\circ - 50 \cos 45^\circ - 80 \cos 60^\circ$

$R_x = -51.40 \, \text{ lb}$

$R_x = 51.40 \, \text{ lb to the left}$
 

$R_y = \Sigma F_y$

$R_y = 30 \sin 37^\circ + 50 \sin 45^\circ - 80 \sin 60^\circ$

$R_y = -15.87 \, \text{ lb}$

$R_y = 15.87 \, \text{ lb downward}$
 

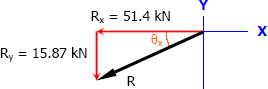$R = \sqrt{{R_x}^2 + {R_y}^2}$

$R = \sqrt{51.40^2 + 15.87^2}$

$R = 53.79 \, \text{ lb}$
 

$\tan \theta_x = \dfrac{R_y}{R_x} = \dfrac{15.87}{51.40}$

$\theta_x = 17.16^\circ$
 

Thus, the net force on the ring is 53.79 lb downward to the left at θ_x = 17.16°.