014 Solving for force with given resultant

Part a: The resultant is 500N to the right along the x-axis

By Cosine law of the shaded triangle
$P^2 = 200^2 + 500^2 - 2(200)(500) \cos \theta$

$P^2 = 200^2 + 500^2 - 2(200)(500)(\frac{12}{13})$

$P = 324.63 \, \text{ N}$           answer
 

 

By Sine law
$\dfrac{P}{\sin \theta} = \dfrac{200}{\sin \alpha}$

$\sin \alpha = \dfrac{200 \sin \theta}{P} = \dfrac{200 (\frac{5}{13})}{324.63}$

$\alpha = 13.71^\circ$           answer
 

Part b: The resultant is 500 N upward to the right with a slope of 3 horizontal to 4 vertical
 

 

$R_x = 500(\frac{3}{5}) = 300 \, \text{ N}$

$R_y = 500(\frac{4}{5}) = 400 \, \text{ N}$
 

$R_x = P \cos \alpha + 200(\frac{12}{13})$

$300 = P \cos \alpha + 184.61$

$P \cos \alpha = 115.39$

$P = \dfrac{115.39}{\cos \alpha}$
 

$R_y = P \sin \alpha - 200(\frac{5}{13})$

$400 = P \sin \alpha - 76.92$

$P \sin \alpha = 476.92$

$\left( \dfrac{115.39}{\cos \alpha} \right)\sin \alpha = 476.92$

$115.38 \tan \alpha = 476.92$

$\tan \alpha = 4.1335$

$\alpha = 76.4^\circ$           answer
 

$P = \dfrac{115.39}{\cos 76.4^\circ}$

$P = 490.68 \, \text{ N}$           answer
 

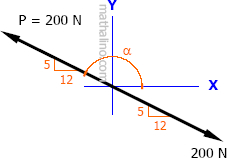Part c: The resultant is zero

The resultant is zero if P and the 200 N force are equal in magnitude, oppositely directed, and collinear.
 

$\alpha = 180^\circ - \arctan \frac{5}{12}$

$\alpha = 157.38^\circ$
 

Thus, P = 200 N at α = 157.38°           answer