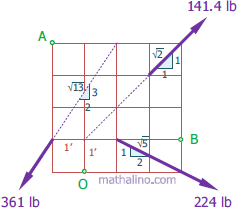
$R_x = \Sigma F_x$
$R_x = 141.4(\frac{1}{\sqrt{2}}) + 224(\frac{2}{\sqrt{5}}) - 361(\frac{2}{\sqrt{13}})$
$R_x = 100.09 \, \text{ lb to the right}$
$R_y = \Sigma F_y$
$R_y = 141.4(\frac{1}{\sqrt{2}}) - 224(\frac{1}{\sqrt{5}}) - 361(\frac{3}{\sqrt{13}})$
$R_y = -300.56 \, \text{ lb}$
$R_y = 300.56 \, \text{ lb downward}$
$R = \sqrt{{R_x}^2 + {R_y}^2}$
$R = \sqrt{100.09^2 + 300.56^2}$
$R = 316.79 \, \text{ lb downward to the right}$
$\tan \theta_x = \dfrac{R_y}{R_x}$
$\tan \theta_x = \dfrac{300.56}{100.09}$
$\theta_x = 71.58^\circ$
$M_O = -141.4(\frac{1}{\sqrt{2}})(1) - 224(\frac{1}{\sqrt{5}})(3) + 361(\frac{2}{\sqrt{13}})(1) + 361(\frac{3}{\sqrt{13}})(1)$
$M_O = 100.1 \text{ lb}\cdot\text{ft counterclockwise}$
Equivalent force through O and couple through A and B are shown in the figure below:

The resultant force's
The resultant force's magnitude and angle passing through O is correct, but I think it needs to be drawn correctly. The force needs to be drawn steeper than what is shown in the drawing to show the correct angle base on the angles value.