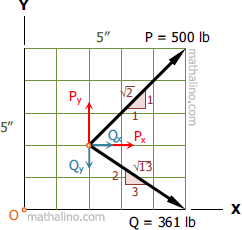
$P_x = 500(\frac{1}{\sqrt{2}}) = 353.55 \, \text{ lb}$ to the right
$P_y = 500(\frac{1}{\sqrt{2}}) = 353.55 \, \text{ lb}$ upward
$Q_x = 361(\frac{3}{\sqrt{13}}) = 300.37 \, \text{ lb}$ to the right
$Q_y = 361(\frac{2}{\sqrt{13}}) = 200.25 \, \text{ lb}$ downward
$M_O = 5Q_y = 5(200.25)$
$M_O = 1001.25 \, \text{ lb}\cdot\text{in.}$ clockwise
$R_x = P_x + Q_x = 353.55 + 300.37$
$R_x = 653.92 \, \text{ lb}$ to the right
$R_y = P_y - Q_y = 353.55 - 200.25$
$R_y = 153.3 \, \text{ lb}$ upward
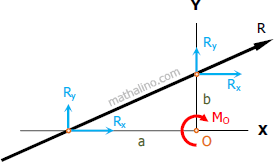x-intercept of the resultant
$aR_y = M_O$
$a(153.3) = 1001.25$
$a = 6.53 \, \text{ in.}$ to the left of point O answer
y-intercept of the resultant
$bR_x = M_O$
$b(653.92) = 1001.25$
$b = 1.53 \, \text{ in.}$ above point O answer
