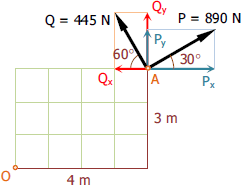
$R_x = P_x - Q_x$
$R_x = 890 \cos 30^\circ - 445 \cos 60^\circ$
$R_x = 548.26 \, \text{ N}$ (to the right)
$R_y = P_y + Q_y$
$R_y = 890 \sin 30^\circ + 445 \sin 60^\circ$
$R_y = 830.38 \, \text{ N}$ (upward)
$M_O = 4R_y - 3R_x$
$M_O = 4(830.38) - 3(548.26)$
$M_O = 1676.74 \, \text{ N}\cdot\text{m}$ (counterclockwise) answer
The moment of resultant about O can be solved actually without the use of Rx and Ry. The moment effect of the components of R is the same as the combined moment effect of the components P and Q. Thus, $M_O = 4P_y + 4Q_y + 3Q_x - 3P_x$. Try it.
You can also find Mo by finding the magnitude of R and its moment arm about point O. Moment arm is the perpendicular distance between the line of action of R and point O.
