The Ellipse
Definition of Ellipse
Ellipse is the locus of point that moves such that the sum of its distances from two fixed points called the foci is constant. The constant sum is the length of the major axis, 2a.
General Equation of the Ellipse
From the general equation of all conic sections, A and C are not equal but of the same sign. Thus, the general equation of the ellipse is Ax2 + Cy2 + Dx + Ey + F = 0 or
Standard Equations of Ellipse
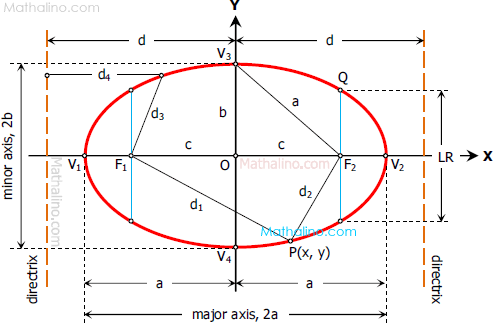
From the figure above,
$d_1 = \sqrt{(x + c)^2 + y^2}$ and
$d_2 = \sqrt{(x - c)^2 + y^2}$
From the definition above,
$d_1 + d_2 = 2a$
$\sqrt{(x + c)^2 + y^2} + \sqrt{(x - c)^2 + y^2} = 2a$
$\sqrt{(x + c)^2 + y^2} = 2a - \sqrt{(x - c)^2 + y^2}$
Square both sides
$(x + c)^2 + y^2 = 4a^2 - 4a\sqrt{(x - c)^2 + y^2} + [ \, (x - c)^2 + y^2 \, ]$
$x^2 + 2xc + c^2 + y^2 = 4a^2 - 4a\sqrt{(x - c)^2 + y^2} + x^2 - 2xc + c^2 + y^2$
$2xc = 4a^2 - 4a\sqrt{(x - c)^2 + y^2} - 2xc$
$4a\sqrt{(x - c)^2 + y^2} = 4a^2 - 4xc$
$a\sqrt{(x - c)^2 + y^2} = a^2 - xc$
Square again both sides
$a^2 [ \, (x - c)^2 + y^2 \, ] = (a^2 - xc)^2$
$a^2 [ \, x^2 - 2xc + c^2 + y^2 \, ] = a^4 - 2a^2xc + x^2c^2$
$a^2x^2 - 2a^2xc + a^2c^2 + a^2y^2 = a^4 - 2a^2xc + x^2c^2$
$a^2x^2 + a^2c^2 + a^2y^2 = a^4 + x^2c^2$
$a^2x^2 - x^2c^2 + a^2y^2 = a^4 - a^2c^2$
$(a^2 - c^2)x^2 + a^2y^2 = a^2(a^2 - c^2)$
From triangle OV3F2 (see figure above)
$c^2 + b^2 = a^2$
$a^2 - c^2 = b^2$
Thus,
$b^2x^2 + a^2y^2 = a^2b^2$
Divide both sides by a2b2
$\dfrac{b^2x^2}{a^2b^2} + \dfrac{a^2y^2}{a^2b^2} = \dfrac{a^2b^2}{a^2b^2}$
$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$
The above equation is the standard equation of the ellipse with center at the origin and major axis on the x-axis as shown in the figure above. Below are the four standard equations of the ellipse. The first equation is the one we derived above.
- Log in to post comments
