The Parabola
Definition of Parabola
Parabola is the locus of point that moves such that it is always equidistant from a fixed point and a fixed line. The fixed point is called focus and the fixed line is called directrix.
General Equations of Parabola
From the general equation of all conic sections, either $A$ or $C$ is zero to form a parabolic section.
For $A = 0$, the equation will reduce to $Cy^2 + Dx + Ey + F = 0$ or
It is a parabola with axis horizontal, e.g., open to the right or open to the left.
For $C = 0$, the equation will reduce to $Ax^2 + Dx + Ey + F = 0$ or
It is a parabola with axis vertical, e.g., open upward or open downward.
Standard Equations of Parabola
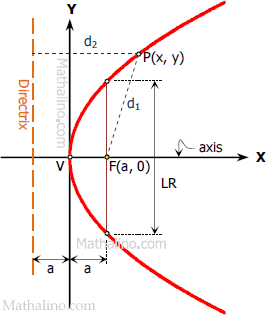
From the definition
$d_1 = d_2$
${d_1}^2 = {d_2}^2$
$(x - a)^2 + (y - 0)^2 = (x + a)^2$
$(x^2 - 2ax + a^2) + y^2 = x^2 + 2ax + a^2$
$-2ax + y^2 = 2ax$
$y^2 = 4ax$
The equation we just derived was with reference to the figure shown above, thus, it is a parabola with vertex at the origin and open to the right.
Hint: To avoid memorizing the eight (8) standard equations of parabola, we will reduce it to only two (2) as follows:
$(x - h)^2 = \pm 4a(y - k)$
Note that (h, k) is (0, 0) at the origin. Use positive (+) for open upward and rightward parabolas, negative (-) for open downward and leftward parabolas.
Elements of Parabola
- Focus is located at distance $a$ from vertex in the direction of parabola’s opening.
- Directrix is at distance $a$ from the vertex. It is a straight line located at the opposite side of parabola’s opening.
- Vertex is the point extremity of parabola, i.e. highest point for open downward, lowest point for open upward, rightmost point for leftward, and leftmost point for rightward. The coordinates of vertex is denoted as (h, k).
- Axis is the line of symmetry of parabola. It contains both the focus and the vertex and always perpendicular to the directrix.
- Latus Rectum, denoted by $LR$, is a line perpendicular to the axis, passing through the focus and terminates on the parabola itself. The total length of $LR$ is $4a$ ($LR = 4a$), where $a$ stands for the distance from focus to vertex.
- Eccentricity of parabola is always equal to 1 ($e = 1$). Thus, parabola can also be defined as a conic section of eccentricity equal to 1.
- Log in to post comments
