The Hyperbola
Definition
Hyperbola can be defined as the locus of point that moves such that the difference of its distances from two fixed points called the foci is constant. The constant difference is the length of the transverse axis, 2a.
General Equation
From the general equation of any conic (A and C have opposite sign, and can be A > C, A = C, or A C.)
$Ax^2 - Cy^2 + Dx + Ey + F = 0 \,$ or
Back to top
Standard Equations
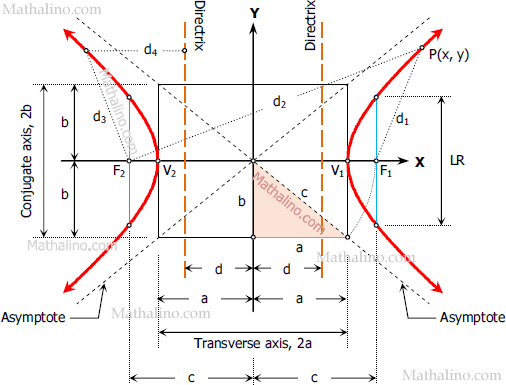
From the definition:
$d_2 - d_1 = 2a$
$\sqrt{(x + c)^2 + (y - 0)^2} - \sqrt{(x - c)^2 + (y - 0)^2} = 2a$
$\sqrt{(x + c)^2 + y^2} = 2a + \sqrt{(x - c)^2 + y^2}$
$(x + c)^2 + y^2 = 4a^2 + 4a\sqrt{(x - c)^2 + y^2} + [ \, (x - c)^2 + y^2 \, ]$
$(x + c)^2 = 4a^2 + 4a\sqrt{(x - c)^2 + y^2} + (x - c)^2$
$x^2 + 2xc + c^2 = 4a^2 + 4a\sqrt{(x - c)^2 + y^2} + x^2 - 2cx + c^2$
$4xc - 4a^2 = 4a\sqrt{(x - c)^2 + y^2}$
$xc - a^2 = a\sqrt{(x - c)^2 + y^2}$
$(xc - a^2)^2 = a^2 [ \, (x - c)^2 + y^2 \, ]$
$x^2c^2 - 2xca^2 + a^4 = a^2 [ \, (x - c)^2 + y^2 \, ]$
$x^2c^2 - 2xca^2 + a^4 = a^2 [ \, x^2 - 2xc + c^2 + y^2 \, ]$
$x^2c^2 - 2xca^2 + a^4 = a^2x^2 - 2xca^2 + a^2c^2 + a^2y^2$
$x^2c^2 + a^4 = a^2x^2 + a^2c^2 + a^2y^2$
$(x^2c^2 - a^2x^2) - a^2y^2 = a^2c^2 - a^4$
$(c^2 - a^2)x^2 - a^2y^2 = a^2(c^2 - a^2)$
From the figure:
$c^2 = a^2 + b^2$
$c^2 - a^2 = b^2$
Thus,
$b^2x^2 - a^2y^2 = a^2b^2$
$\dfrac{b^2x^2}{a^2b^2} - \dfrac{a^2y^2}{a^2b^2} = \dfrac{a^2b^2}{a^2b^2}$
$\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1$
The equation we just derived above is the standard equation of hyperbola with center at the origin and transverse axis on the x-axis (see figure above). Below are the four standard equations of hyperbola. The first equation is the one we derived just derived.
Back to top
Elements of Hyperbola
- Center (h, k). At the origin, (h, k) is (0, 0).
- Transverse axis = 2a and conjugate axis = 2b
- Location of foci c, relative to the center of hyperbola.
$c = \sqrt{a^2 + b^2}$ - Latus rectum, LR
$LR = \dfrac{2b^2}{a}$ - Eccentricity, e
The eccentricity of hyperbola is always greater than one.
$e = \dfrac{c}{a} > 1.0$ - Location of directrix d relative to the center of hyperbola.
$d = \dfrac{a}{e}$ or $d = \dfrac{a^2}{c}$ - Equation of asymptotes.
$y - k = \pm m(x - h)$
where
m is (+) for upward asymptote and m is (-) for downward.
m = b/a if the transverse axis is horizontal and
m = a/b if the transverse axis is vertical
- Log in to post comments
