Elements of Ellipse

Elements of the ellipse are shown in the figure below.
 

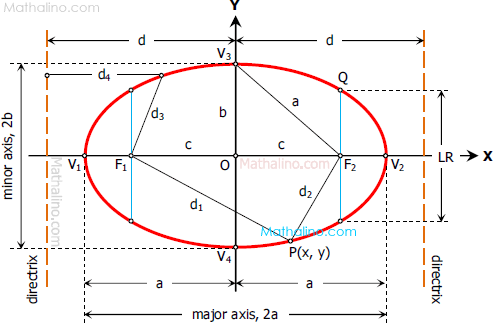
1. Center (h, k). At the origin, (h, k) is (0, 0).
2. Semi-major axis = a and semi-minor axis = b.
3. Location of foci c, with respect to the center of ellipse. $c = \sqrt{a^2 - b^2}$.
4. Length latus rectum, LR
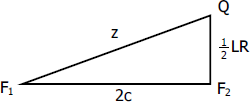   Consider the right triangle F₁QF₂:

Based on the definition of ellipse
$z + \frac{1}{2}LR = 2a$

$z = 2a - \frac{1}{2}LR$

$z = \dfrac{4a - LR}{2}$
 

By Pythagorean Theorem
$(2c)^2 + (\frac{1}{2}LR)^2 = z^2$

$4c^2 + \frac{1}{4}(LR)^2 = \left( \dfrac{4a - LR}{2} \right)^2$

$4c^2 + \frac{1}{4}(LR)^2 = \dfrac{(4a - LR)^2}{4}$

$16c^2 + (LR)^2 = (4a - LR)^2$

$16c^2 + (LR)^2 = 16a^2 - 8a(LR) + (LR)^2$

$16c^2 = 16a^2 - 8a(LR)$

$8a(LR) = 16a^2 - 16c^2$

$LR = \dfrac{16a^2 - 16c^2}{8a}$

$LR = \dfrac{16(a^2 - c^2)}{8a}$

$LR = \dfrac{2b^2}{a}$

You can also find the same formula for the length of latus rectum of ellipse by using the definition of eccentricity.
 

5. Eccentricity, e
   $e = \dfrac{\text{distance from focus to ellipse}}{\text{distance from ellipse to directrix}}$
    

   From the figure of the ellipse above,
   $e = \dfrac{d_3}{d_4} = \dfrac{a}{d} = \dfrac{a - c}{d - a}$

   From
   $\dfrac{a}{d} = \dfrac{a - c}{d - a}$

   $ad - a^2 = ad - cd$

   $d = a^2 / c$
    

   Thus,
   $e = \dfrac{a}{d} = \dfrac{a}{a^2 / c}$

   $e = \dfrac{c}{a} \lt 1.0$

    

6. Location of directrix d, with respect to the center of ellipse.

   From the derivation of eccentricity,

   $d = \dfrac{a}{e} \, \text{ or } d = \dfrac{a^2}{c}$