Problem 40
The base of a right triangle grows 2 ft/sec, the altitude grows 4 ft/sec. If the base and altitude are originally 10 ft and 6 ft, respectively, find the time rate of change of the base angle, when the angle is 45°.
 

Problem 39
A balloon, leaving the ground 60 ft from an observer, rises 10 ft/sec. How fast is the angle of elevation of the line of sight increasing, after 8 seconds?
 

Problem 38
A ship, moving 8 mi/hr, sails north for 30 min, then turns east. If a searchlight at the point of departure follows the ship, how fast is the light rotating 2 hr after the start.
 

Problem 37
A ladder 15 ft long leans against a vertical wall. If the top slides down at 2 ft/sec, how fast is the angle of elevation of the ladder decreasing, when the lower end is 12 ft from the wall?
 

Problem 26
A corridor 4 ft wide opens into a room 100 ft long and 32 ft wide, at the middle of one side. Find the length of the longest thin rod that can be carried horizontally into the room.

Problem 24
Find the area of the largest rectangle that can be cut from a circular quadrant as in Fig. 76.
 

Problem 23
A sphere is cut in the form of a right pyramid with a square base. How much of the material can be saved?
 

Problem 22
A sphere of radius a is dropped into a conical vessel full of water. Find the altitude of the smallest cone that will permit the sphere to be entirely submerged.
 

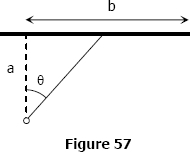Problem 19
A man on an island a miles south of a straight beach wishes to reach a point on shore b miles east of his present position. If he can row r miles per hour and walk w miles per hour, in what direction should he row, to reach his destination as soon as possible? See Fig. 57.