37 - A ladder sliding downward

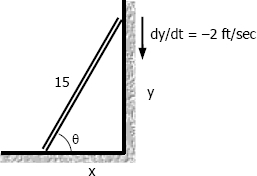
$\theta = \arcsin \dfrac{y}{15}$

$\dfrac{d\theta}{dt} = \dfrac{\dfrac{dy/dt}{15}}{\sqrt{1 - \left( \dfrac{y}{15} \right)^2}}$

$\dfrac{d\theta}{dt} = \dfrac{\dfrac{dy/dt}{15}}{\sqrt{1 - \left( \dfrac{y}{15} \right)^2}}$

$\dfrac{d\theta}{dt} = \dfrac{dy/dt}{15\sqrt{1 - \dfrac{y^2}{225}}}$
 

when $x = 12$
$y = \sqrt{15^2 - 12^2}$

$y = 9 \,\, \text{ ft}$
 

$\dfrac{d\theta}{dt} = \dfrac{-2}{15\sqrt{1 - \dfrac{9^2}{225}}}$

$\dfrac{d\theta}{dt} = \dfrac{-2}{15\sqrt{1 - \dfrac{81}{225}}}$

$\dfrac{d\theta}{dt} = \dfrac{-2}{15\sqrt{1 - \dfrac{9}{25}}}$

$\dfrac{d\theta}{dt} = \dfrac{-2}{15\sqrt{\dfrac{16}{25}}}$

$\dfrac{d\theta}{dt} = \dfrac{-2}{15 \left( \dfrac{4}{5} \right)}$

$\dfrac{d\theta}{dt} = \dfrac{-2}{12}$

$\dfrac{d\theta}{dt} = -\dfrac{1}{6} \, \text{ rad/sec}$           answer

The negative sign indicates that the angle is decreasing.

(Using Trigonometric Function)
$\sin \theta = y/15$

$\cos \theta \dfrac{d\theta}{dt} = \dfrac{dy/dt}{15}$
 

when $x = 12$

$\cos \theta = 12/15$
 

Thus,
$\dfrac{12}{15} \, \dfrac{d\theta}{dt} = \dfrac{-2}{15}$

$\dfrac{d\theta}{dt} = \dfrac{-2}{15} \times \dfrac{15}{12}$

$\dfrac{d\theta}{dt} = -\dfrac{1}{6} \, \text{ rad/sec}$       (okay!)