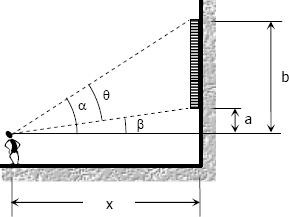
From the figure:
$\theta = \alpha - \beta$
$\tan \theta = \tan (\alpha - \beta)$
$\tan \theta = \dfrac{\tan \alpha - \tan \beta}{1 + \tan \alpha \, \tan \beta}$
$\tan \theta = \dfrac{\dfrac{b}{x} - \dfrac{a}{x}}{1 + \dfrac{b}{x} \left( \dfrac{a}{x} \right)}$
$\tan \theta = \dfrac{\dfrac{b - a}{x}}{\dfrac{x^2 + ab}{x^2}}$
$\tan \theta = \dfrac{b - a}{\dfrac{x^2 + ab}{x}}$
$\tan \theta = \dfrac{(b - a)x}{x^2 + ab}$
$\theta = \arctan \dfrac{(b - a)x}{x^2 + ab}$
$\dfrac{d\theta}{dx} = \dfrac{\dfrac{(x^2 + ab)(b - a) - (b - a)x(2x)}{(x^2 + ab)^2}}{1 + \left[ \dfrac{(b - a)x}{x^2 + ab} \right]^2} = 0$
$\dfrac{(x^2 + ab)(b - a) - (b - a)x(2x)}{(x^2 + ab)^2} = 0$
$(x^2 + ab)(b - a) - (b - a)x(2x) = 0$
$(b - a) \, [ \, (x^2 + ab) - 2x^2 \, ] = 0$
$(x^2 + ab) - 2x^2 = 0$
$ab - x^2 = 0$
$ab = x^2$
$x = \sqrt{ab}$ answer
