49-51 Ship sailing east and turned N 30d E

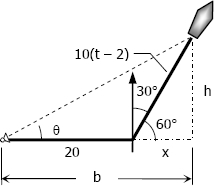
$h = 10(t - 2) \sin 60^\circ$

$h = 10(t - 2)\left( \dfrac{\sqrt{3}}{2} \right)$

$h = 5\sqrt{3}(t - 2)$
 

$x = 10(t - 2) \cos 60^\circ$

$x = 10(t - 2)(1/2)$

$x = 5(t - 2)$
 

$b = 20 + x = 20 + 5(t - 2)$

$b = 20 + 5t - 10 = 5t + 10$

$b = 5(t + 2)$
 

$\theta = \arctan \dfrac{h}{b}$

$\theta = \arctan \dfrac{5\sqrt{3}(t - 2)}{5(t + 2)}$

$\theta = \arctan \dfrac{\sqrt{3}(t - 2)}{t + 2}$

$\dfrac{d\theta}{dt} = \dfrac{\dfrac{(t + 2)\sqrt{3} - \sqrt{3}(t - 2)(1)}{(t + 2)^2}}{1 + \left[ \dfrac{\sqrt{3}(t - 2)}{t + 2} \right]^2}$

$\dfrac{d\theta}{dt} = \dfrac{\dfrac{t\sqrt{3} + 2\sqrt{3} - t\sqrt{3} + 2\sqrt{3}}{(t + 2)^2}}{1 + \dfrac{3(t - 2)^2}{(t + 2)^2}}$

$\dfrac{d\theta}{dt} = \dfrac{\dfrac{4\sqrt{3}}{(t + 2)^2}}{\dfrac{(t + 2)^2 + 3(t - 2)^2}{(t + 2)^2}}$

$\dfrac{d\theta}{dt} = \dfrac{4\sqrt{3}}{(t + 2)^2 + 3(t - 2)^2}$
 

(a) 4 hours after the start, t = 4
$\dfrac{d\theta}{dt} = \dfrac{4\sqrt{3}}{(4 + 2)^2 + 3(4 - 2)^2}$

$\dfrac{d\theta}{dt} = \dfrac{4\sqrt{3}}{36 + 12}$

$\dfrac{d\theta}{dt} = \dfrac{4\sqrt{3}}{48}$

$\dfrac{d\theta}{dt} = \frac{1}{12}\sqrt{3} \, \text{ rad/sec}$           answer
 

(b) Just after the turn, t = 2
$\dfrac{d\theta}{dt} = \dfrac{4\sqrt{3}}{(2 + 2)^2 + 3(2 - 2)^2}$

$\dfrac{d\theta}{dt} = \dfrac{4\sqrt{3}}{16 + 0}$

$\dfrac{d\theta}{dt} = \dfrac{4\sqrt{3}}{16}$

$\dfrac{d\theta}{dt} = \frac{1}{4}\sqrt{3} \, \text{ rad/sec}$           answer

Let r = rate or speed of ship
$h = r (t - 2) \sin 60^\circ$

$h = \frac{1}{2}\sqrt{3}r (t - 2)$
 

$x = r (t - 2) \cos 60^\circ$

$x = \frac{1}{2}(t - 2)$
 

$b = 2r + x = 2r + \frac{1}{2} r (t - 2)$

$b = 2r + \frac{1}{2}rt - r = \frac{1}{2}r t + r$

$b = \frac{1}{2}r(t + 2)$
 

$\theta = \arctan \dfrac{h}{b} = \arctan \dfrac{\frac{1}{2}\sqrt{3}r (t - 2)}{\frac{1}{2}r(t + 2)}$

$\theta = \arctan \dfrac{\sqrt{3}(t - 2)}{t + 2}$
 

The above value of angle θ did not include the speed of the ship r. The derivative of θ in terms of time t will of course be independent from r. Problem 49 is a derivative of θ in terms of time t.