45 - Angle of elevation of the the kite's cord

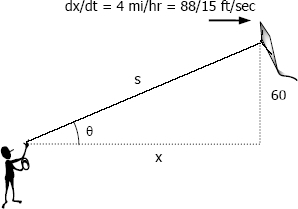
$\theta = \arctan \dfrac{60}{x}$

$\dfrac{d\theta}{dt} = \dfrac{\dfrac{-60\dfrac{dx}{dt}}{x^2}}{1 + \left( \dfrac{60}{x} \right)^2}$

$\dfrac{d\theta}{dt} = \dfrac{-60\dfrac{dx}{dt}}{x^2\left( 1 + \dfrac{3600}{x^2} \right)}$

$\dfrac{d\theta}{dt} = \dfrac{-60\dfrac{dx}{dt}}{x^2\left( 1 + \dfrac{3600}{x^2} \right)}$

$\dfrac{d\theta}{dt} = \dfrac{-60\dfrac{dx}{dt}}{x^2 + 3600}$
 

when s = 100 ft
$x = \sqrt{100^2 - 60^2}$

$x = 80 \, \text{ ft}$
 

$\dfrac{d\theta}{dt} = \dfrac{-60(88/15)}{80^2 + 3600}$

$\dfrac{d\theta}{dt} = \dfrac{-352}{10\,000}$

$\dfrac{d\theta}{dt} = -\dfrac{22}{625} \,\, \text{ rad/sec}$

$\dfrac{d\theta}{dt} = \dfrac{22}{625} \, \text{ rad/sec decreasing}$           answer

$\tan \theta = \dfrac{60}{x}$

$\sec^2 \theta \, \dfrac{d\theta}{dt} = \dfrac{-60 \dfrac{dx}{dt}}{x^2}$

$\dfrac{1}{\cos^2 \theta} \, \dfrac{d\theta}{dt} = - \dfrac{60 \dfrac{dx}{dt}}{x^2}$

$\dfrac{d\theta}{dt} = -\dfrac{60 \cos^2 \theta}{x^2}\,\dfrac{dx}{dt}$
 

When s = 100 ft
x = 80 ft (see Solution 45 above)
cos θ = 80/100 = 4/5
 

$\dfrac{d\theta}{dt} = -\dfrac{60 (4/5)^2}{80^2}\times(88/15)$

$\dfrac{d\theta}{dt} = -\dfrac{22}{625} \, \text{ rad/sec}$           (okay!)