Regular Pyramid

A regular pyramid is one whose base is a regular polygon whose center coincides with the foot of the perpendicular dropped from the vertex to the base.

Properties of a Regular Pyramid

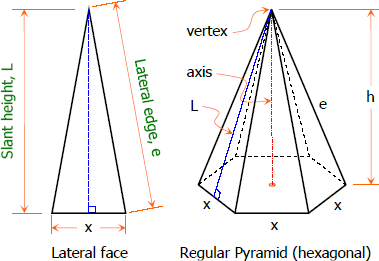The edges of a regular pyramid are equal; it is denoted by e.
The lateral faces of a regular pyramid are congruent isosceles triangles (see figure).
The altitudes of the lateral faces of a regular pyramid are equal. It is the slant height of the regular pyramid and is denoted by L.
The altitude of the regular pyramid is perpendicular to the base. It is equal to length of the axis and is denoted by h.
The vertex of regular pyramid is directly above the center of its base when the pyramid is oriented as shown in the figure.
If a cutting plane is passed parallel to the base of regular pyramid, the pyramid cut off is a regular pyramid similar to the original pyramid.

Formula for regular pyramid

Area of the base (note: the base is a regular polygon), A_b

$A_b = \dfrac{n}{2}xr$

$A_b = \dfrac{n}{2}R^2 \sin \theta$

For more information about the two formulas above, see The Regular Polygon.

Area of one Lateral Face, A₁

$A_1 = xL$

Lateral Area, A_L

$A_L = nA_1$

$A_L = \dfrac{n}{2}xL$

$A_L = \dfrac{PL}{2}$

Total Area, A_T

$A_T = A_b + A_L$

Length of lateral edge, e

$e = \sqrt{R^2 + h^2}$

Slant height, L

$L = \sqrt{r^2 + h^2}$

$L = \sqrt{e^2 - (x/2)^2}$

Volume, V

$V = \frac{1}{3}A_b \, h$

$V = \dfrac{n}{6}xr \, h$

$V = \dfrac{n}{6}R^2h \, \sin \theta$

Where
A_b = area of the base (regular polygon)
A₁ = area of one lateral face
A_L = lateral area
A_T = total area
x = length of side of the base
h = altitude of pyramid (this is the length of axis of the pyramid)
L = slant height of pyramid (this is the altitude of triangular face)
P = perimeter of the base
e = length of lateral edge
For x, R, r, n, and θ, see The Regular Polygon.

Navigation

Recent comments