Volume of pyramid cut from a sphere

$r^2 + 6^2 = 9^2$

$r^2 = 45$
 

$\theta = \dfrac{360^\circ}{n}$
 

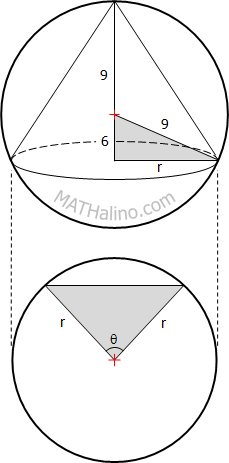Base area of pyramid
$A_b = n \times \frac{1}{2}r^2 \sin \theta$

$A_b = n \times \frac{1}{2}(45) \sin \left( \dfrac{360^\circ}{n} \right)$

$A_b = 22.5n \sin \left( \dfrac{360^\circ}{n} \right)$
 

Volume of pyramid
$V = \frac{1}{3}A_bh$

$V = \dfrac{1}{3} \times \left[ 22.5n \sin \left( \dfrac{360^\circ}{n} \right) \right] \times 15$

$V = 112.5n \sin \left( \dfrac{360^\circ}{n} \right)$
 

Part (a) Square pyramid: n = 4
$V = 112.5(4) \sin \left( \dfrac{360^\circ}{4} \right)$

$V = 450 ~ \text{in.}^3$           answer
 

Part (b) Pentagonal pyramid: n = 5
$V = 112.5(5) \sin \left( \dfrac{360^\circ}{5} \right)$

$V = 534.97 ~ \text{in.}^3$           answer
 

Part (c) Hexagonal pyramid: n = 6
$V = 112.5(6) \sin \left( \dfrac{360^\circ}{6} \right)$

$V = 584.57 ~ \text{in.}^3$           answer
 

Part (d) Octagonal pyramid: n = 8
$V = 112.5(8) \sin \left( \dfrac{360^\circ}{8} \right)$

$V = 636.40 ~ \text{in.}^3$           answer