The Pyramid
A pyramid is a polyhedron with a polygon base of any shape, and all other faces are triangles which have common vertex.
Properties of a Pyramid
 The lateral faces are all triangles meeting at the vertex of the pyramid
The lateral faces are all triangles meeting at the vertex of the pyramid- The altitude of the pyramid is shortest distance between the vertex and the base. It is the drop distance from the vertex perpendicular to the base.
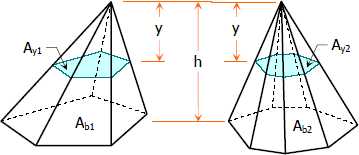
- If a cutting plane parallel to the base will pass through the pyramid, the smaller pyramid thus formed is similar to the original pyramid. By similar solids, $\dfrac{A_b}{A_y} = \dfrac{h^2}{y^2}$.
- If two pyramids have equal base area and equal altitude, any section made by a cutting plane parallel to the base are equal. From the figure, if $A_{b1} = A_{b2}$ then $A_{y1} = A_{y2}$.
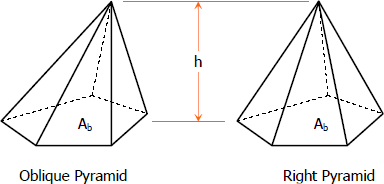
- The pyramid is said to be a right pyramid if the vertex is directly above the centroid of the base, otherwise it is an oblique pyramid
Name of a Pyramid
The name of a pyramid is according to its base. If the base is square, it is called square pyramid, and if the base is pentagon, it is called pentagonal pyramid. Triangular pyramid is also called tetrahedron.
Formulas for Pyramid
The area of the base is according to the shape of the base polygon. There is no specific formula for this except for regular pyramids.
The lateral area of the pyramid is equal to the sum of the areas of lateral faces that are triangles. There is no specific formula for this except for right regular pyramids.
$A_T = A_b + A_L$
$V = \frac{1}{3}A_b \, h$
Tags
- Log in to post comments
