Problem
Determine the volume of a regular tetrahedron of edge 2 ft.
| A. 1.54 ft3 | C. 1.34 ft3 |
| B. 1.01 ft3 | D. 0.943 ft3 |
Problem 40
When a liquid freezes, it changes into a mass of solid bodies, each of which has a definite geometric form and is known as a crystal. Crystals are always bounded by plane surfaces, which are arranged in an orderly fashion with reference to imaginary lines drawn through the crystal and called its area. Every crystal has therefore a definite geometric form. Compare the volumes of crystals, one in the shape of a hexagonal right prism 'a' units on a side and '2a' units in altitude, and the other in the shape of two oppositely directed hexagonal regular pyramids, each 'a' units high with a common base 'a' units on a side.
Problem 27
One hundred and fifty posts are used in fencing a lawn. Each post is built in the form of frustum of a pyramid surmounted by a pyramid whose lower base is common with the upper base of the frustum. The height of the pyramidal top is 2 in. and the common base is a square 4 in. on an edge. The lower base of the frustum has an edge of 6 in. If the overall height of each is 6 ft., how much concrete will be used in making the posts?
Example 016
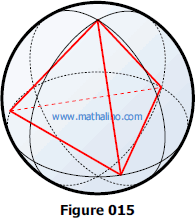
Find the area of the surface and the volume of the sphere circumscribed about a regular tetrahedron of edge 25 cm. See Figure 015.
Example 011
A layer of equal spheres is in the form of a square. The spheres are arranged so that each sphere is tangent to every one adjacent to it. In the spaces between sets of 4 adjacent spheres, other spheres rest, equal in size to the original. These spheres form in turn a second layer on top of the first. Successive layers of this sort form a pyramidal pile with a single sphere resting on top. If the bottom layer contains 16 spheres, what is the height of the pile in terms of the common radius r of the spheres?
Problem 23
A sphere is cut in the form of a right pyramid with a square base. How much of the material can be saved?
Regular tetrahedron is one of the regular polyhedrons. It is a triangular pyramid whose faces are all equilateral triangles.
A regular pyramid is one whose base is a regular polygon whose center coincides with the foot of the perpendicular dropped from the vertex to the base.
A pyramid is a polyhedron with a polygon base of any shape, and all other faces are triangles which have common vertex.
This is a group of solids in which the volume is equal to one-third of the product of base area and altitude. There are two solids that belong to this group; the pyramid and the cone.
