The Regular Tetrahedron
Regular tetrahedron is one of the regular polyhedrons. It is a triangular pyramid whose faces are all equilateral triangles.
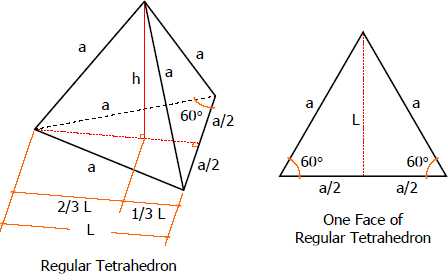
Properties of a Regular Tetrahedron
- There are four faces of regular tetrahedron, all of which are equilateral triangles.
- There are a total of 6 edges in regular tetrahedron, all of which are equal in length.
- There are four vertices of regular tetrahedron, 3 faces meets at any one vertex.
- A regular tetrahedron can circumscribe a sphere that is tangent to all the faces of the tetrahedron.
- A regular tetrahedron can be inscribed in a sphere that passes through all the vertices of tetrahedron.
- The center of the inscribed sphere, the center of the circumscribing sphere, and the center of the regular tetrahedron itself are coincidence.
Formulas for Regular Tetrahedron
$A_b = \frac{1}{2}a^2 \sin \theta$
$A_b = \frac{1}{2}a^2 ( \frac{\sqrt{3}}{2} )$
Total area, AT
$A_T = 4A_b$
$A_T = 4 ( a^2 \sqrt{3} / 4 )$
Slant height, L
$L = a \sin 60^\circ$
$L = a ( \frac{\sqrt{3}}{2} )$
Altitude, h
$(\frac{2}{3}L)^2 + h^2 = a^2$
$\frac{4}{9}L^2 + h^2 = a^2$
$\frac{4}{9}(a \sqrt{3} / 2)^2 + h^2 = a^2$
$\frac{4}{9}( \frac{3}{4} a^2 ) + h^2 = a^2$
$\frac{1}{3}a^2 ) + h^2 = a^2$
$h^2 = \frac{2}{3}a^2 )$
$h = a \sqrt{\frac{2}{3}}$
$h = a \sqrt{\frac{2}{3} \times \frac{3}{3}}$
$h = a \sqrt{\frac{6}{9}}$
Volume, V
$V = \frac{1}{3}A_b \, h$
$V = \dfrac{1}{3} \left( \dfrac{a^2 \sqrt{3}}{4} \right) \left( \dfrac{a\sqrt{6}}{3} \right)$
$V = \dfrac{a^3 \sqrt{18}}{36}$
$V = \dfrac{a^3 \sqrt{9(2)}}{3(12)}$
$V = \dfrac{a^3 (3 \sqrt{2})}{3(12)}$
- Log in to post comments
