$\tan \theta = \frac{2}{4}$
$\theta = 26.56^\circ$
$30^\circ + \theta = 30 + 26.56^\circ$
$30^\circ + \theta = 56.56^\circ$
Apply Cosine law to triangle ABC
$b^2 = 2^2 + 3^2 - 2(2 \times 3) \cos (30^\circ + 90^\circ)$
$b = \sqrt{19} \, \text{m} = 4.36 \, \text{m}$
$\dfrac{b}{\sin (30^\circ + 90^\circ)} = \dfrac{2}{\sin \alpha}$
$\sin \alpha = \dfrac{2 \sin 120^\circ}{\sqrt{19}}$
$\alpha = 23.41^\circ$
At Joint A
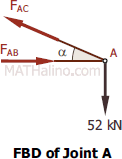$\Sigma F_V = 0$
$F_{AC} \sin \alpha = 52$
$F_{AC} \sin 23.41^\circ = 52$
$F_{AC} = 131 \, \text{kN}$ tension
$\Sigma F_H = 0$
$F_{AB} = F_{AC} \cos \alpha$
$F_{AB} = 131 \cos 23.41^\circ$
$F_{AB} = 120 \, \text{kN}$ compression
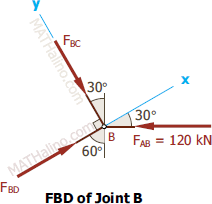At Joint B
$\Sigma F_y = 0$
$F_{BC} = 120 \sin 30^\circ$
$F_{BC} = 60 \, \text{kN}$ compression
$\Sigma F_x = 0$
$F_{BD} = 120 \cos 30^\circ$
$F_{BD} = 104 \, \text{kN}$ compression
At Joint C
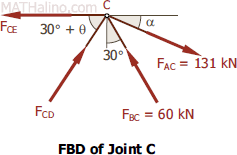$\Sigma F_V = 0$
$F_{CD} \sin (30^\circ + \theta) + 60 \cos 30^\circ = 131 \sin \alpha$
$F_{CD} \sin 56.56^\circ + 60 \cos 30^\circ = 131 \sin 23.41^\circ$
$F_{CD} = 0$
$\Sigma F_H = 0$
$F_{CE} + 60 \sin 30^\circ = 131 \cos \alpha$
$F_{CE} + 60 \sin 30^\circ = 131 \cos 23.41^\circ$
$F_{CE} = 90 \, \text{kN}$ tension
Summary
AC = 131 kN tension
AB = 120 kN compression
BC = 60 kN compression
BD = 104 kN compression
CD = 0
CE = 90 kN tension
