Problem 407 Cantilever Truss - Method of Joints

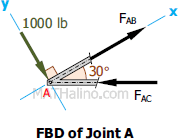
At Joint A
$\Sigma F_y = 0$

$F_{AC} \sin 30^\circ = 1000$

$F_{AC} = 2000 \, \text{lb}$   compression
 

$\Sigma F_x = 0$

$F_{AB} = F_{AC} \cos 30^\circ$

$F_{AB} = 2000 \cos 30^\circ$

$F_{AB} = 1732.05 \, \text{lb}$   tension
 

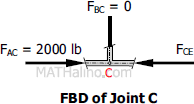At Joint C
$\Sigma F_V = 0$

$F_{BC} = 0$
 

$\Sigma F_H = 0$

$F_{CE} = 2000 \, \text{lb}$   compression
 

At Joint B
 

 

$\Sigma F_y = 0$

$F_{BE} \sin 60^\circ = 1000$

$F_{BE} = 1154.70 \, \text{lb}$   compression
 

From the FBD of the whole truss shown below
$b = 3a \sin 30^\circ$

$b = 1.5a$
 

 

Solve for the reaction at support H
$\Sigma M_G = 0$

$R_H(b) = 1000(3a) + 1000(2a) + 1000(a)$

$R_H(1.5a) = 6000a$

$R_H = 4000 \, \text{lb}$
 

Thus,
$F_{EH} = 4000 \, \text{lb}$   compression
 

At Joint E
 

 

$\Sigma F_H = 0$

$F_{EF} \cos 60^\circ + 1154.70 \sin 60^\circ + 2000 = 4000$

$F_{EF} = 2000 \, \text{lb}$   tension
 

$\Sigma F_V = 0$

$F_{DE} + 1154.70 \cos 60^\circ = F_{EF} \sin 60^\circ$

$F_{DE} + 1154.70 \cos 60^\circ = 2000 \sin 60^\circ$

$F_{DE} = 1154.7 \, \text{lb}$   compression
 

We may check F_DE by Method of Sections (Optional)
 

 

$\Sigma M_G = 0$

$F_{DE}(a \cos 30^\circ) = 1000a$

$F_{DE} = 1154.7 \, \text{lb}$   compression       Check!
 

Summary (Answers)
AB = 1732.05 lb tension
BE = 1154.70 lb compression
DE = 1154.70 lb compression