Solving for force in members AB, BD, and CD
$\Sigma M_H = 0$
$12R_A = 9(30) + 6(30) + 3(90)$
$R_A = 60 \, \text{kN}$
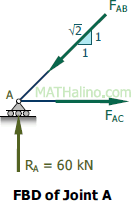At Joint A
$\Sigma F_V = 0$
$\frac{1}{\sqrt{2}}F_{AB} = 60$
$F_{AB} = 84.85 \, \text{kN}$ compression answer
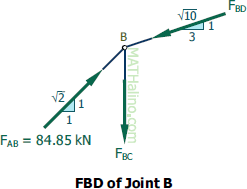At Joint B
$\Sigma F_H = 0$
$\frac{3}{\sqrt{10}}F_{BD} = \frac{1}{\sqrt{2}}(84.85)$
$F_{BD} = 63.24 \, \text{kN}$ compression answer
$\Sigma F_V = 0$
$F_{BC} + \frac{1}{\sqrt{10}}F_{BD} = \frac{1}{\sqrt{2}}(84.85)$
$F_{BC} + \frac{1}{\sqrt{10}}(63.24) = \frac{1}{\sqrt{2}}(84.85)$
$F_{BC} = 40 \, \text{kN}$ tension
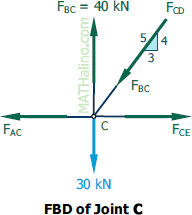At Joint C
$\Sigma F_V = 0$
$\frac{4}{5}F_{CD} + 30 = 40$
$F_{CD} = 12.5 \, \text{kN}$ compression answer
Summary
AB = 84.85 kN compression
BD = 63.24 kN compression
CD = 12.5 kN compression
Solving for force in members FH, DF, and DG
$\Sigma M_A = 0$
$12R_H = 3(30) + 6(30) + 9(90)$
$R_H = 90 \, \text{kN}$
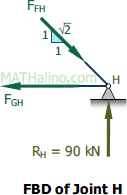At Joint H
$\Sigma F_V = 0$
$\frac{1}{\sqrt{2}}F_{FH} = 90$
$F_{FH} = 127.28 \, \text{kN}$ compression answer
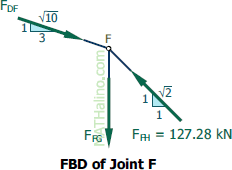At Joint F
$\Sigma F_H = 0$
$\frac{3}{\sqrt{10}}F_{DF} = \frac{1}{\sqrt{2}}(127.28)$
$F_{DF} = 94.87 \, \text{kN}$ compression answer
$\Sigma F_H = 0$
$F_{FG} + \frac{1}{\sqrt{10}}F_{DF} = \frac{1}{\sqrt{2}}(127.28)$
$F_{FG} + \frac{1}{\sqrt{10}}(94.87) = \frac{1}{\sqrt{2}}(127.28)$
$F_{FG} = 60 \, \text{kN}$ tension
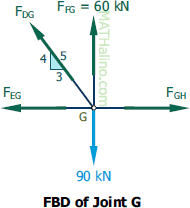At Joint G
$\Sigma F_V = 0$
$\frac{4}{5}F_{DG} + 60 = 90$
$F_{DG} = 37.5 \, \text{kN}$ tension answer
Summary
FH = 127.28 kN compression
DF = 94.87 kN compression
DG = 37.5 kN tension
