$\Sigma M_D = 0$
$2xR_A = 450x$
$R_A = 225 \, \text{N}$
$\Sigma M_A = 0$
$2xV_D = 450x + (450 \sin 30^\circ)(2x)$
$V_D = 450 \, \text{N}$
$\Sigma F_H = 0$
$H_D = 450 \cos 30^\circ = 389.71 \, \text{N}$
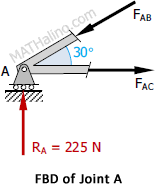At Joint A
$\Sigma F_V = 0$
$F_{AB} \sin 30^\circ = 225$
$F_{AB} = 450 \, \text{N}$
$\Sigma F_H = 0$
$F_{AC} = F_{AB} \cos 30^\circ = 450 \cos 30^\circ$
$F_{AC} = 389.71 \, \text{N}$
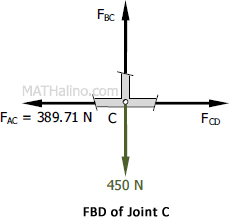At Joint C
$\Sigma F_V = 0$
$F_{BC} = 450 \, \text{N}$
$\Sigma F_H = 0$
$F_{CD} = 389.71 \, \text{N}$
At Joint B
$\Sigma F_H = 0$
$F_{BD} \cos 30^\circ = 450 \cos 30^\circ + 450 \cos 30^\circ$
$F_{BD} = 900 \, \text{N}$
$\Sigma F_V = 0$
$F_{BD} \sin 30^\circ + 450 \sin 30^\circ = 450 + 450 \sin 30^\circ$
$F_{BD} = 900 \, \text{N}$ Check!
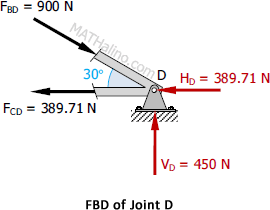At Joint D
$\Sigma F_V = 0$
$450 = 900 \sin 30^\circ$
$450 = 450$ Check!
$\Sigma F_H = 0$
$900 \cos 30^\circ = 389.71 + 389.71$
$779.42 = 779.42$ Check!
Summary
AB = 450 N compression
AC = 389.71 N tension
BC = 450 N tension
BD = 900 N compression
CD = 389.71 N tension
