By symmetry
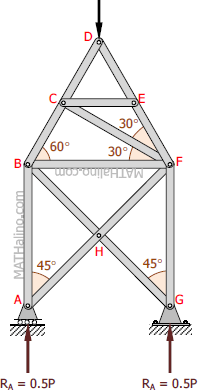
$R_A = R_G = 0.5P$
From joint D
$\Sigma F_H = 0$
$F_{CD} \cos 60^\circ = F_{DE} \cos 60^\circ$
$F_{CD} = F_{DE}$
$\Sigma F_V = 0$
$F_{CD} \sin 60^\circ + F_{DE} \sin 60^\circ = P$
$F_{DE} \sin 60^\circ + F_{DE} \sin 60^\circ = P$
$2F_{DE} \sin 60^\circ = P$
$F_{DE} = 0.5774P \, \text{ compression}$
Hence,
$F_{CD} = 0.5774P \, \text{ compression}$
From joint C
$F_{BC} = F_{CD}$
$F_{BC} = 0.5774P \, \text{ compression}$
$F_{CE} = 0$
$F_{CF} = 0$
From joint E
$F_{EF} = F_{DE}$
$F_{EF} = 0.5774P \, \text{ compression}$
From joint A
$F_{AB} = R_A$
$F_{AB} = 0.5P \, \text{ compression}$
$F_{AH} = 0$
From joint G
$F_{FG} = R_G$
$F_{FG} = 0.5P \, \text{ compression}$
$F_{GH} = 0$
From joint H
$F_{FH} = 0$
$F_{BH} = 0$
From joint B
$\Sigma F_H = 0$
$F_{BF} = F_{BC} \cos 60^\circ$
$F_{BF} = 0.5774P \cos 60^\circ$
$F_{BF} = 0.2887P \, \text{ tension}$
Summary
