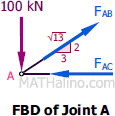
At Joint A
$\Sigma F_V = 0$
$F_{AB}(\frac{2}{\sqrt{13}}) = 100$
$F_{AB} = 180.2776 \, \text{kN}$ tension answer
$\Sigma F_H = 0$
$F_{AC} = \frac{3}{\sqrt{13}}F_{AB}$
$F_{AC} = \frac{3}{\sqrt{13}}(180.2776)$
$F_{AC} = 150 \, \text{kN}$ compression answer
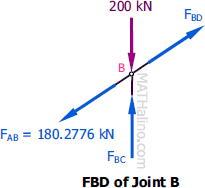At Joint B
By inspection
$F_{BD} = 180.2776 \, \text{kN}$ tension answer
$F_{BC} = 200 \, \text{kN}$ compression
Length of member DE
$\dfrac{DE}{AE} = \dfrac{FG}{AG}$
$\dfrac{DE}{20} = \dfrac{20}{30}$
$DE = \frac{40}{3} \, \text{m}$
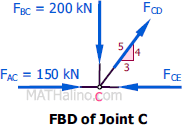At Joint C
$\Sigma F_V = 0$
$F_{CD}(\frac{4}{5}) = 200$
$F_{CD} = 250 \, \text{kN}$ tension answer
$\Sigma F_H = 0$
$F_{CE} = 150 + \frac{3}{5}F_{CD}$
$F_{CE} = 150 + \frac{3}{5}(250)$
$F_{CE} = 300 \, \text{kN}$ compression answer
The fastest way to solve for BD, CD, and CE is by method of sections. From the figure below:
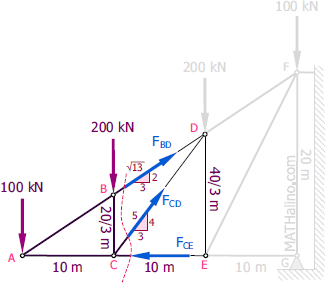$\Sigma M_C = 0$
$\frac{3}{\sqrt{13}}F_{BD}(\frac{20}{3}) = 100(10)$
$F_{BD} = 180.2776 \, \text{kN}$ tension Check!
$\Sigma M_A = 0$
$\frac{4}{5}F_{CD}(10) = 200(10)$
$F_{CD} = 250 \, \text{kN}$ tension Check!
$\Sigma M_D = 0$
$F_{CE}(\frac{40}{3}) = 100(20) + 200(10)$
$F_{CE} = 300 \, \text{kN}$ compression Check!
Summary of Answers
AB = 180.2776 kN tension
AC = 150 kN compression
BD = 180.2776 kN tension
CD = 250 kN tension
CE = 300 kN compression
Solving for other members
$\Sigma M_E = 0$
$\frac{3}{\sqrt{13}}F_{DF}(\frac{40}{3}) = 100(20) + 200(10)$
$F_{DF} = 360.5551 \, \text{kN}$ tension
$\Sigma M_A = 0$
$\frac{2}{\sqrt{5}}F_{EF}(20) = 200(20) + 200(10)$
$F_{EF} = 335.4102 \, \text{kN}$ tension
$\Sigma M_F = 0$
$20F_{EG} = 100(30) + 200(20) + 200(10)$
$F_{EG} = 450 \, \text{kN}$ compression
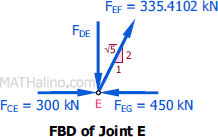At Joint E
$\Sigma F_V = 0$
$F_{DE} = \frac{2}{\sqrt{5}}(335.4102)$
$F_{DE} = 300 \, \text{kN}$ compression
With 200 kN loads moved from B and D to C and E, respectively
At Joint A
$\Sigma F_V = 0$
$F_{AB}(\frac{2}{\sqrt{13}}) = 100$
$F_{AB} = 180.2776 \, \text{kN}$ tension (no changes)
$\Sigma F_H = 0$
$F_{AC} = \frac{3}{\sqrt{13}}F_{AB}$
$F_{AC} = \frac{3}{\sqrt{13}}(180.2776)$
$F_{AC} = 150 \, \text{kN}$ compression (no changes)
From the figure below
$\Sigma M_C = 0$
$\frac{3}{\sqrt{13}}F_{BD}(\frac{20}{3}) = 100(10)$
$F_{BD} = 180.2776 \, \text{kN}$ tension (no changes)
$\Sigma M_A = 0$
$\frac{4}{5}F_{CD}(10) = 200(10)$
$F_{CD} = 250 \, \text{kN}$ tension (no changes)
$\Sigma M_D = 0$
$F_{CE}(\frac{40}{3}) = 100(20) + 200(10)$
$F_{CE} = 300 \, \text{kN}$ compression (no changes)
At Joint B
By inspection
$F_{BC} = 0$ (changed)
From the figure below
$\Sigma M_E = 0$
$\frac{3}{\sqrt{13}}F_{DF}(\frac{40}{3}) = 100(20) + 200(10)$
$F_{DF} = 360.5551 \, \text{kN}$ tension (no changes)
$\Sigma M_A = 0$
$\frac{2}{\sqrt{5}}F_{EF}(20) = 200(20) + 200(10)$
$F_{EF} = 335.4102 \, \text{kN}$ tension (no changes)
$\Sigma M_F = 0$
$20F_{EG} = 100(30) + 200(20) + 200(10)$
$F_{EG} = 450 \, \text{kN}$ compression (no changes)
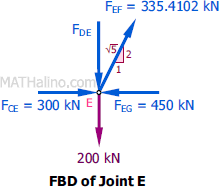At Joint E
$\Sigma F_V = 0$
$F_{DE} + 200 = \frac{2}{\sqrt{5}}(335.4102)$
$F_{DE} = 100 \, \text{kN}$ compression (changed)
Summary of Changes in Internal Forces
- BC from 200 kN compression to 0
- DE from 300 kN compression to 100 kN compression
