$\Sigma M_F = 0$
$11R_A = 7(50) + 3(30)$
$R_A = 40 \, \text{ kN}$
$\Sigma M_A = 0$
$11R_F = 4(50) + 8(30)$
$R_F = 40 \, \text{ kN}$
At joint A
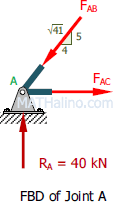$\Sigma F_V = 0$
$\frac{5}{\sqrt{41}}F_{AB} = R_A$
$\frac{5}{\sqrt{41}}F_{AB} = 40$
$F_{AB} = 51.22 \, \text{ kN compression}$
$\Sigma F_H = 0$
$F_{AC} = \frac{4}{\sqrt{41}}F_{AB}$
$F_{AC} = \frac{4}{\sqrt{41}}(51.22)$
$F_{AC} = 32 \, \text{ kN tension}$
At joint B
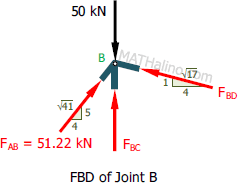$\Sigma F_H = 0$
$\frac{4}{\sqrt{17}}F_{BD} = \frac{4}{\sqrt{41}}F_{AB}$
$\frac{4}{\sqrt{17}}F_{BD} = \frac{4}{\sqrt{41}}(51.22)$
$F_{BD} = 32.98 \, \text{ kN compression}$
$\Sigma F_V = 0$
$F_{BC} + \frac{5}{\sqrt{41}}F_{AB} + \frac{1}{\sqrt{17}}F_{BD} = 50$
$F_{BC} + \frac{5}{\sqrt{41}}(51.22) + \frac{1}{\sqrt{17}}(32.98) = 50$
$F_{BC} = 2 \, \text{ kN compression}$
At joint C
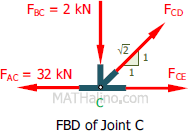$\Sigma F_V = 0$
$\frac{1}{\sqrt{2}}F_{CD} = F_{BC}$
$\frac{1}{\sqrt{2}}F_{CD} = 2$
$F_{CD} = 2.83 \, \text{ kN tension}$
$\Sigma F_H = 0$
$F_{CE} + \frac{1}{\sqrt{2}}F_{CD} = F_{AC}$
$F_{CE} + \frac{1}{\sqrt{2}}(2.83) = 32$
$F_{CE} = 30 \, \text{ kN tension}$
At joint E
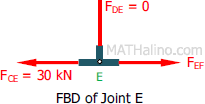$\Sigma F_H = 0$
$F_{EF} = F_{CE}$
$F_{EF} = 30 \, \text{ kN tension}$
$\Sigma F_V = 0$
$F_{DE} = 0$
At joint D
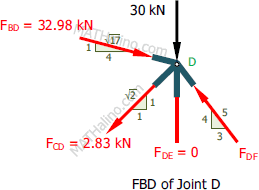$\Sigma F_H = 0$
$\frac{3}{5}F_{DF} + \frac{1}{\sqrt{2}}F_{CD} = \frac{4}{\sqrt{17}}F_{BD}$
$\frac{3}{5}F_{DF} + \frac{1}{\sqrt{2}}(2.83) = \frac{4}{\sqrt{17}}(32.98)$
$F_{DF} = 50 \, \text{ kN compression}$
$\Sigma F_V = 0$
$\frac{4}{5}F_{DF} = \frac{1}{\sqrt{17}}F_{BD} + \frac{1}{\sqrt{2}}F_{CD} + 30$
$\frac{4}{5}(50) = \frac{1}{\sqrt{17}}(32.98) + \frac{1}{\sqrt{2}}(2.83) + 30$
$40 = 40$ check
At joint F
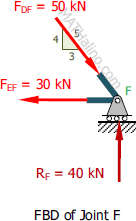$\Sigma F_V = 0$
$\frac{4}{5}F_{DF} = R_A$
$\frac{4}{5}(50) = 40$
$40 = 40$ check
$\Sigma F_H = 0$
$F_{EF} = \frac{3}{5}F_{DF}$
$F_{EF} = \frac{3}{5}(50)$
$30 = 30$ check
Summary
