$\Sigma M_E = 0$
$20R_A = 1000(15) + 4000(10) + 3000(5)$
$R_A = 3500 \, \text{lb}$
$M_E = 0$
$20R_E = 1000(5) + 4000(10) + 3000(15)$
$R_E = 4500 \, \text{lb}$
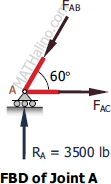At Joint A
$\Sigma F_V = 0$
$F_{AB} \sin 60^\circ = 3500$
$F_{AB} = 4041.45 \, \text{lb}$ compression
$\Sigma F_H = 0$
$F_{AC} = F_{AB} \cos 60^\circ$
$F_{AC} = 4041.45 \cos 60^\circ$
$F_{AC} = 2020.72 \, \text{lb}$ tension
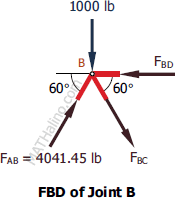At Joint B
$\Sigma F_V = 0$
$F_{BC} \sin 60^\circ + 1000 = 4041.45 \sin 60^\circ$
$F_{BC} = 2886.75 \, \text{lb}$ tension
$\Sigma F_H = 0$
$F_{BD} = 4041.45 \cos 60^\circ + F_{BC} \cos 60^\circ$
$F_{BD} = 4041.45 \cos 60^\circ + 2886.75 \cos 60^\circ$
$F_{BD} = 3464.10 \, \text{lb}$ compression
At Joint C
$\Sigma F_V = 0$
$F_{CD} \sin 60^\circ + 2886.75 \sin 60^\circ = 4000$
$F_{CD} = 1732.05 \, \text{lb}$ tension
$\Sigma F_H = 0$
$F_{CE} + F_{CD} \cos 60^\circ = 2020.72 + 2886.75 \cos 60^\circ$
$F_{CE} + 1732.05 \cos 60^\circ = 2020.72 + 2886.75 \cos 60^\circ$
$F_{CE} = 2598.07 \, \text{lb}$ tension
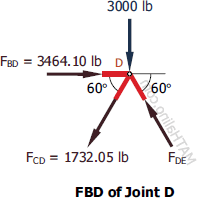At Joint D
$\Sigma F_V = 0$
$F_{DE} \sin 60^\circ = 1732.05 \sin 60^\circ + 3000$
$F_{DE} = 5196.15 \, \text{lb}$ compression
$\Sigma F_H = 0$
$F_{DE} \cos 60^\circ + 1732.05 \cos 60^\circ = 3464.10$
$5196.15 \cos 60^\circ + 1732.05 \cos 60^\circ = 3464.10$
$3464.10 = 3464.10$ Check!
At Joint E
$\Sigma F_V = 0$
$5196.15 \sin 60^\circ = 4500$
$4500 = 4500$ Check!
$\Sigma F_H = 0$
$5196.15 \cos 60^\circ = 2598.07$
$2598.07 = 2598.07$ Check!
Summary
AB = 4041.45 lb compression
AC = 2020.72 lb tension
BC = 2886.75 lb tension
BD = 3464.10 lb compression
CD = 1732.05 lb tension
CE = 2598.07 lb tension
DE = 5196.15 lb compression
