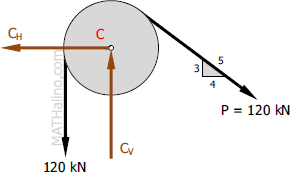
The load is lifted at constant velocity (in dynamic equilibrium), thus, the forces involve is similar to forces under static equilibrium.
$\Sigma F_V = 0$
$C_V = 120 + 120(\frac{3}{5})$
$C_V = 192 \, \text{kN}$
$\Sigma F_H = 0$
$C_H = 120(\frac{4}{5})$
$C_H = 96 \, \text{kN}$
By symmetry of vertical forces
$R_A = D_V = \frac{1}{2}(192)$
$R_A = D_V = 96 \, \text{kN}$
$\Sigma F_H = 0$
$D_H = 96 \, \text{kN}$
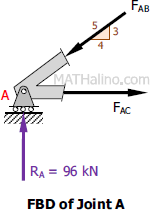At Joint A
$\Sigma F_V = 0$
$F_{AB}(\frac{3}{5}) = 96$
$F_{AB} = 160 \, \text{kN}$
$\Sigma F_H = 0$
$F_{AC} = \frac{4}{5}F_{AB} = \frac{4}{5}(160)$
$F_{AC} = 128 \, \text{kN}$
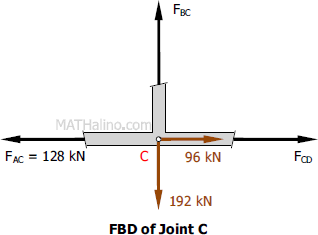At Joint C
$\Sigma F_V = 0$
$F_{BC} = 192 \, \text{kN}$
$\Sigma F_H = 0$
$F_{CD} + 96 = 128$
$F_{CD} = 32 \, \text{kN}$
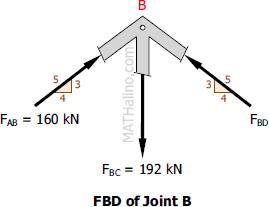At Joint B
$\Sigma F_H = 0$
$F_{BD}(\frac{4}{5}) = 160(\frac{4}{5})$
$F_{BD} = 160 \, \text{kN}$
$\Sigma F_V = 0$
$F_{BD}(\frac{3}{5}) + 160(\frac{3}{5}) = 192$
$160(\frac{3}{5}) + 160(\frac{3}{5}) = 192$
$192 = 192$ Check!
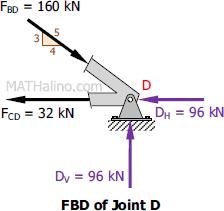At Joint D
$\Sigma F_V = 0$
$96 = 160(\frac{3}{5})$
$96 = 96$ Check!
$\Sigma F_H = 0$
$32 + 96 = 160(\frac{4}{5})$
$128 = 128$ Check!
Summary
AB = 160 kN compression
AC = 128 kN tension
BC = 192 kN tension
CD = 32 kN tension
BD = 160 kN compression
With the roller support at D and the hinge support at A
