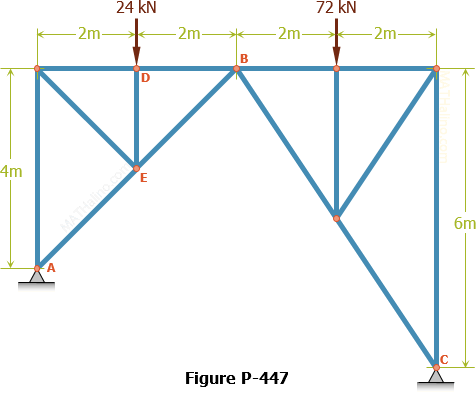
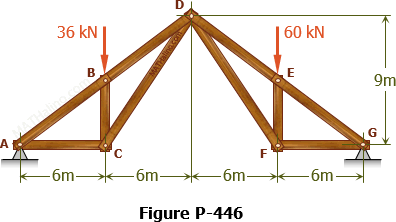
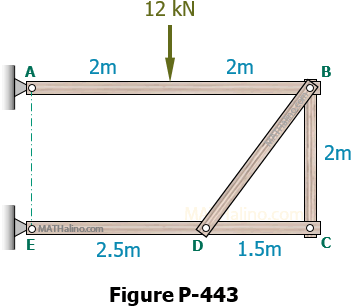
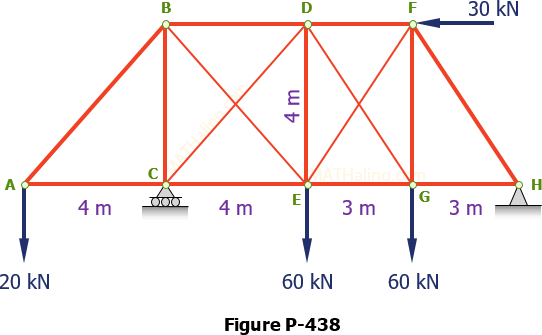
Method of Sections

Problem 447
The truss are joined as shown in Figure P-447 to form a three-hinged arch. Determine the horizontal and vertical components of the hinge force at B and then determine the type and magnitude of force in bars BD and BE.
 

Problem 446
A three-hinged arch is composed of two trusses hinged together at D in Figure P-446. Compute the components of the reaction at A and find the forces acting in bars AB and AC.
 

Problem 443
The frame shown in Figure P-443 is hinged to rigid supports at A and E. Find the components of the hinge forces A and E and the forces in members BC and BD.
 

Problem 438
The center diagonals of the truss in Figure P-438 can support tension only. Compute the force in each center diagonal and the force in BC, DE, and FG.
 

Problem 437
The center panel of the truss in Figure P-437 contains two flexible cables. What load P will cause a compressive force of 20 kN in BD? Then determine which tension diagonal BE or CD is acting and the force in it.
 

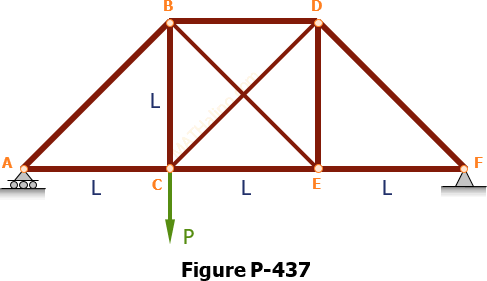
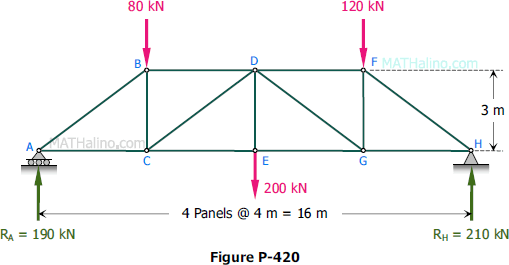
In Figure P-420, assume that counter diagonals act from B to E and from E to F in addition to the counter diagonals CD and DG shown in the figure. Assuming that these counter diagonals can support tension only, determine which diagonals are acting and the force in each.
 

Problem 435
For the transmission tower shown in Fig. P-435, determine the force in member CJ.
 

Problem 434
Compute the force in bars GI, GH, EH, and HI for the scissors truss shown in Fig. P-433.
 

Problem 433
Compute the forces in bars AB, AC, DF, and DE of the scissors truss shown in Fig. P433.
 

Problem 432
Use the method of sections to compute the force in members AB, AD, BC, and BD of the truss shown in Fig. P-432.