From the FBD of the whole system
$\Sigma M_C = 0$
$2A_H + 8A_V = 6(24) + 2(72)$
$2A_H + 8A_V = 288$
$A_H + 4A_V = 144$ ← Equation (1)
$\Sigma M_A = 0$
$2C_H + 2(24) + 6(72) = 8C_V$
$2C_H + 480 = 8C_V$
$2C_H - 8C_V = -480$
$C_H - 4C_V = -240$ ← Equation (2)
From the FBD of the section to the left of B
$\Sigma M_B = 0$
$4A_H + 2(24) = 4A_V$
$4A_H - 4A_V = -48$
$A_H - A_V = -12$ ← Equation (3)
$\Sigma M_A = 0$
$4B_H = 4B_V + 2(24)$
$4B_H - 4B_V = 48$
$B_H - B_V = 12$ ← Equation (4)
From the FBD of the section to the right of B
$\Sigma M_B = 0$
$6C_H + 2(72) = 4C_V$
$6C_H - 4C_V = -144$
$3C_H - 2C_V = -72$ ← Equation (5)
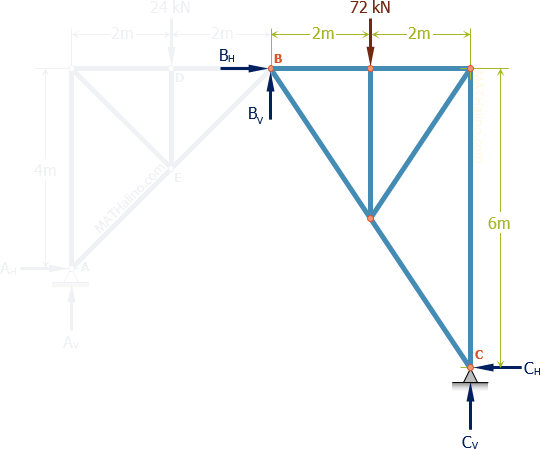
$\Sigma M_C = 0$
$6B_H + 4B_V = 2(72)$
$6B_H + 4B_V = 144$
$3B_H + 2B_V = 72$ ← Equation (6)
From Equation (1) and Equation (3)
$A_H = 19.2 ~ \text{kN}$
$A_V = 31.2 ~ \text{kN}$
From Equation (2) and Equation (5)
$C_H = 19.2 ~ \text{kN}$
$C_V = 64.8 ~ \text{kN}$
From Equation (4) and Equation (6)
$B_H = 19.2 ~ \text{kN}$
$B_V = 7.2 ~ \text{kN}$
Checking for Reactions:
$\Sigma F_H = 0$
$19.2 - 19.2 = 0$ (okay!)
$\Sigma F_V = 0$
$31.2 + 64.8 - 24 - 72 = 0$ (okay!)
From the FBD of the Section to the Left of M-M
$\Sigma M_A = 0$
$4F_{BD} = 2(24)$
$F_{BD} = 12 ~ \text{kN compression}$
$\Sigma F_V = 0$
$F_{BE} \sin 45^\circ + 24 = 31.2$
$F_{BE} = 7.2\sqrt{2} ~ \text{kN}$
$F_{BE} = 10.182 ~ \text{kN compression}$
Checking:
From the FBD of the Section to the Right of N-N
$\Sigma M_C = 0$
$6F_1 = 2(72)$
$F_1 = 24 ~ \text{kN}$
$\Sigma F_V = 0$
$\frac{3}{\sqrt{13}}F_2 + 64.8 = 72$
$F_2 = 2.4\sqrt{13} ~ \text{kN}$
$F_2 = 8.653 ~ \text{kN tension}$
From the FBD of Joint B
$\Sigma F_V = 0$
$F_{BE} \sin 45^\circ = \frac{3}{\sqrt{13}}F_2$
$7.2\sqrt{2} \sin 45^\circ = \frac{3}{\sqrt{13}}\left( 2.4\sqrt{13} \right)$
$7.2 = 7.2$ (okay!)
$\Sigma F_H = 0$
$F_{BD} + F_{BE} \cos 45^\circ + \frac{2}{\sqrt{13}}F_2 = F_1$
$12 + 7.2\sqrt{2} \cos 45^\circ + \frac{2}{\sqrt{13}}\left( 2.4\sqrt{13} \right) = 24$
$24 = 24$ (okay!)
Answer Summary
$B_H = 19.2 ~ \text{kN}$
$B_V = 7.2 ~ \text{kN}$
$F_{BD} = 12 ~ \text{kN compression}$
$F_{BE} = 10.182 ~ \text{kN compression}$
