Problem 05 | Inverse Laplace Transform
Problem 05
Find the inverse transform of $\dfrac{2s^2 + 5s - 6}{s^3 - 3s^2 - 13s + 15}$
- Read more about Problem 05 | Inverse Laplace Transform
- Log in or register to post comments
Problem 04 | Inverse Laplace Transform
Problem 04
Perform the indicated operation: $\mathcal{L}^{-1} \left[ \dfrac{s - 5}{s^2 + s - 6} \right]$
- Read more about Problem 04 | Inverse Laplace Transform
- Log in or register to post comments
Problem 03 | Inverse Laplace Transform
Problem 03
Find the inverse transform of $\dfrac{7}{s^2 + 6}$.
- Read more about Problem 03 | Inverse Laplace Transform
- Log in or register to post comments
Problem 01 | Right Spherical Triangle
Problem
Solve for the spherical triangle whose parts are a = 73°, b = 62°, and C = 90°.
- Read more about Problem 01 | Right Spherical Triangle
- Log in or register to post comments
Oblique Spherical Triangle
Definition of oblique spherical triangle
Spherical triangles are said to be oblique if none of its included angle is 90° or two or three of its included angles are 90°. Spherical triangle with only one included angle equal to 90° is a right triangle.
Sine law
$\dfrac{\sin a}{\sin A} = \dfrac{\sin b}{\sin B} = \dfrac{\sin c}{\sin C}$
- Read more about Oblique Spherical Triangle
- Log in or register to post comments
Right Spherical Triangle
Solution of right spherical triangle
With any two quantities given (three quantities if the right angle is counted), any right spherical triangle can be solved by following the Napier’s rules. The rules are aided with the Napier’s circle. In Napier’s circle, the sides and angle of the triangle are written in consecutive order (not including the right angle), and complimentary angles are taken for quantities opposite the right angle.
- Read more about Right Spherical Triangle
- 2 comments
- Log in or register to post comments
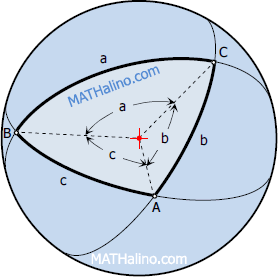
Spherical Trigonometry
Spherical Triangle
Any section made by a cutting plane that passes through a sphere is circle. A great circle is formed when the cutting plane passes through the center of the sphere. Spherical triangle is a triangle bounded by arc of great circles of a sphere.
- Read more about Spherical Trigonometry
- Log in or register to post comments
Problem 544 | Friction on Wedges
Problem 544
The block A in Fig. P-544 supports a load W and is to be raised by forcing the wedge B under it. If the angle of friction is 10° at all surfaces in contact, determine the maximum wedge angle α that will give the wedge a mechanical advantage; i.e., make P less than the weight W of the block.

- Read more about Problem 544 | Friction on Wedges
- Log in or register to post comments
Problem 543 | Friction on Wedges
Problem 543
To adjust the vertical position of a column supporting 200-kN load, two 5° wedges are used as shown in Fig. P-543. Determine the force P necessary to start the wedges is the angle of friction at all contact surfaces is 25°. Neglect friction at the rollers.

- Read more about Problem 543 | Friction on Wedges
- Log in or register to post comments
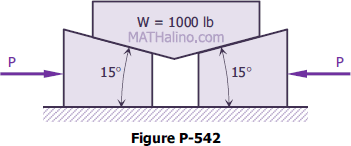
Problem 542 | Friction on Wedges
Problem 542
What force P must be applied to the wedges shown in Fig. P-542 to start them under the block? The angle of friction for all contact surfaces is 10°.
- Read more about Problem 542 | Friction on Wedges
- Log in or register to post comments

Recent comments