Oblique Spherical Triangle

Definition of oblique spherical triangle
Spherical triangles are said to be oblique if none of its included angle is 90° or two or three of its included angles are 90°. Spherical triangle with only one included angle equal to 90° is a right triangle.
 

Sine law
$\dfrac{\sin a}{\sin A} = \dfrac{\sin b}{\sin B} = \dfrac{\sin c}{\sin C}$
 

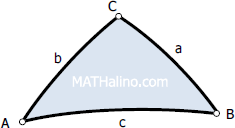
Cosine law for sides
$\cos a = \cos b ~ \cos c + \sin b ~ \sin c ~ \cos A$

$\cos b = \cos a ~ \cos c + \sin a ~ \sin c ~ \cos B$

$\cos c = \cos a ~ \cos b + \sin a ~ \sin b ~ \cos C$
 

Cosine law for angles
$\cos A = -\cos B ~ \cos C + \sin B ~ \sin C ~ \cos a$

$\cos B = -\cos A ~ \cos C + \sin A ~ \sin C ~ \cos b$

$\cos C = -\cos A ~ \cos B + \sin A ~ \sin B ~ \cos c$
 

Napier's analogies
$\dfrac{\sin \frac{1}{2}(A - B)}{\sin \frac{1}{2}(A + B)} = \dfrac{\tan \frac{1}{2}(a - b)}{\tan \frac{1}{2}C}$

$\dfrac{\cos \frac{1}{2}(A - B)}{\cos \frac{1}{2}(A + B)} = \dfrac{\tan \frac{1}{2}(a + b)}{\tan \frac{1}{2}C}$

$\dfrac{\sin \frac{1}{2}(a - b)}{\sin \frac{1}{2}(a + b)} = \dfrac{\tan \frac{1}{2}(A - B)}{\cot \frac{1}{2}c}$

$\dfrac{\cos \frac{1}{2}(a - b)}{\cos \frac{1}{2}(a + b)} = \dfrac{\tan \frac{1}{2}(A + B)}{\cot \frac{1}{2}c}$