Problem
Three squares are drawn so that each will contain a side of regular hexagon as shown in the given figure. If the hexagon has a perimeter of 60 in., compute the area of the region common to the three squares. The required area is the shaded region in the figure.
 

Problem
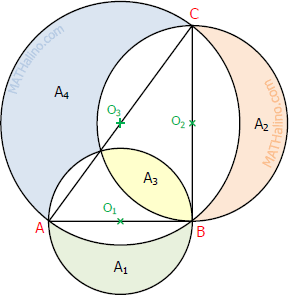
From the figure shown, AB = diameter of circle O₁ = 30 cm, BC = diameter of circle O₂ = 40 cm, and AC = diameter of circle O₃ = 50 cm. Find the shaded areas A₁, A₂, A₃, and A₄ and check that A₁ + A₂ + A₃ = A₄ as stated in the previous problem.
 

Problem
From the figure shown below, O₁, O₂, and O₃ are centers of circles located at the midpoints of the sides of the triangle ABC. The sides of ABC are diameters of the respective circles. Prove that
 

where A₁, A₂, A₃, and A₄ are areas in shaded regions.
 

Problem 719
Determine the centroid of the lines that form the boundary of the shaded area in Fig. P-718.
 

Problem 718
Locate the centroid of the shaded area shown in Fig. P-718.
 

Problem 717
Locate the centroid of the bent wire shown in Fig. P-717. The wire is homogeneous and of uniform cross-section.
 

Problem 716
A slender homogeneous wire of uniform cross section is bent into the shape shown in Fig. P-716. Determine the coordinates of the centroid.
 

Problem 715
Determine the coordinates of the centroid of the area shown in Fig. P-715 with respect to the given axes.
 

Problem 714
The dimensions of the T-section of a cast-iron beam are shown in Fig. P-714. How far is the centroid of the area above the base?
 

Problem 709
Locate the centroid of the area bounded by the x-axis and the sine curve $y = a \sin \dfrac{\pi x}{L}$ from x = 0 to x = L.