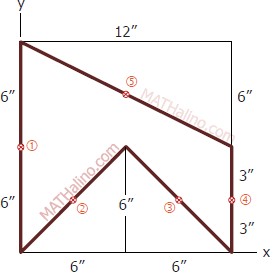
$L_1 = 12 \, \text{ in.}$
$x_1 = 0$
$y_1 = 6$
$L_2 = \sqrt{6^2 + 6^2} = 6\sqrt{2} \, \text{ in.}$
$x_2 = \frac{1}{2}(6) = 3 \, \text{ in.}$
$y_2 = \frac{1}{2}(6) = 3 \, \text{ in.}$
$L_3 = \sqrt{6^2 + 6^2} = 6\sqrt{2} \, \text{ in.}$
$x_3 = 6 + \frac{1}{2}(6) = 9 \, \text{ in.}$
$y_3 = \frac{1}{2}(6) = 3 \, \text{ in.}$
$L_4 = 6 \, \text{ in.}$
$x_4 = 12 \, \text{ in.}$
$y_4 = 3 \, \text{ in.}$
$L_5 = \sqrt{12^2 + 6^2} = 6\sqrt{5} \, \text{ in.}$
$x_5 = \frac{1}{2}(12) = 6 \, \text{ in.}$
$y_5 = 6 + \frac{1}{2}(6) = 9 \, \text{ in.}$
$L = L_1 + L_2 + L_3 + L_4 + L_5$
$L = 12 + 6\sqrt{2} + 6\sqrt{2} + 6 + 6\sqrt{5}$
$L = 48.387 \, \text{ in.}$
$L \, \bar{x} = \Sigma lx$
$48.387\bar{x} = 12(0)+ 6\sqrt{2}(3)+ 6\sqrt{2}(9) + 6(12)+ 6\sqrt{5}(6)$
$\bar{x} = 5.256 \, \text{ in.}$ answer
$L \, \bar{x} = \Sigma lx$
$48.387\bar{y} = 12(6)+ 6\sqrt{2}(3)+ 6\sqrt{2}(3) + 6(3)+ 6\sqrt{5}(9)$
$\bar{y} = 5.408 \, \text{ in.}$ answer
