705 Centroid of parabolic segment by integration

$y^2 = kx$
 

At (a, b)
$b^2 = ka$

$k = \dfrac{b^2}{a}$
 

Thus,
$y^2 = \dfrac{b^2}{a}x$       → equation of parabola

$y = \dfrac{b}{a^{1/2}}x^{1/2}$
 

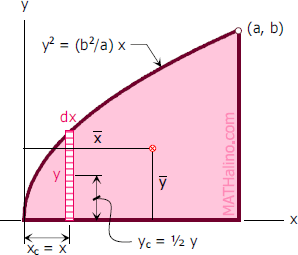Differential area
$dA = y \, dx$

$dA = \dfrac{b}{a^{1/2}}x^{1/2} \, dx$
 

Area of parabola by integration
$\displaystyle A = \int_0^a \left( \dfrac{b}{a^{1/2}}x^{1/2} \right) \, dx$

$\displaystyle A = \dfrac{b}{a^{1/2}}\int_0^a x^{1/2} \, dx$

$A = \dfrac{b}{a^{1/2}}\left[ \dfrac{x^{3/2}}{3/2} \right]_0^a$

$A = \dfrac{2b}{3a^{1/2}}\left[ a^{3/2} - 0^{3/2} \right]$

$A = \frac{2}{3}ab$
 

Location of centroid from the y-axis (x-intercept of centroid)
$\displaystyle A \, \bar{x} = \int_a^b x_c \, dA$

$\displaystyle \frac{2}{3}ab \, \bar{x} = \int_0^a x \left( \dfrac{b}{a^{1/2}}x^{1/2} \right) \, dx$

$\displaystyle \frac{2}{3}ab \, \bar{x} = \dfrac{b}{a^{1/2}}\int_0^a x^{3/2} \, dx$

$\frac{2}{3}ab \, \bar{x} = \dfrac{b}{a^{1/2}} \left[ \dfrac{x^{5/2}}{5/2} \right]_0^a$

$\frac{2}{3}ab \, \bar{x} = \dfrac{2b}{5a^{1/2}} \left[ a^{5/2} - 0^{5/2} \right]$

$\frac{2}{3}ab \, \bar{x} = \frac{2}{5}a^2b$

$\bar{x} = \frac{3}{5}a$           answer
 

Location of centroid from the x-axis (y-intercept of centroid)
$\displaystyle A \, \bar{y} = \int_a^b y_c \, dA$

$\displaystyle \frac{2}{3}ab \, \bar{y} = \int_0^a \frac{1}{2}y (y \, dx)$

$\displaystyle \frac{2}{3}ab \, \bar{y} = \frac{1}{2}\int_0^a y^2 \, dx$

$\displaystyle \frac{2}{3}ab \, \bar{y} = \frac{1}{2}\int_0^a \left( \dfrac{b^2}{a}x \right) \, dx$

$\displaystyle \frac{2}{3}ab \, \bar{y} = \dfrac{b^2}{2a}\int_0^a x \, dx$

$\frac{2}{3}ab \, \bar{y} = \dfrac{b^2}{2a} \left[ \dfrac{x^2}{2} \right]_0^a$

$\frac{2}{3}ab \, \bar{y} = \dfrac{b^2}{4a} \left[ a^2- 0^2 \right]$

$\frac{2}{3}ab \, \bar{y} = \frac{1}{4}ab^2$

$\bar{y} = \frac{3}{8}b$           answer