For the quarter circle
$A_1 = \frac{1}{4}\pi r^2$
$x_1 = \dfrac{4r}{3\pi}$
$y_1 = \dfrac{4r}{3\pi}$
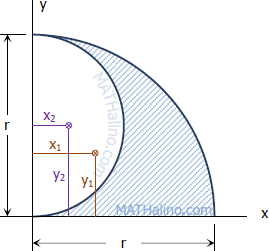For the semicircle
$A_2 = \frac{1}{2}(\frac{1}{4}\pi r^2) = \frac{1}{8}\pi r^2$
$x_2 = \dfrac{4(\frac{1}{2}r)}{3\pi} = \dfrac{2r}{3\pi}$
$y_2 = \frac{1}{2}r$
For the shaded area
$A = A_1 - A_2 = \frac{1}{4}\pi r^2 - \frac{1}{8}\pi r^2$
$A = \frac{1}{8}\pi r^2$
$A\bar{x} = \Sigma ax$
$(\frac{1}{8}\pi r^2) \bar{x} = (\frac{1}{4}\pi r^2) \left( \dfrac{4r}{3\pi} \right) - (\frac{1}{8}\pi r^2) \left( \dfrac{2r}{3\pi} \right)$
$(\frac{1}{8}\pi r^2) \bar{x} = \frac{1}{3}r^3 - \frac{1}{12}r^3$
$(\frac{1}{8}\pi r^2) \bar{x} = \frac{1}{4}r^3$
$\bar{x} = \dfrac{2r}{\pi} = 0.6366r$ answer
$A\bar{y} = \Sigma ay$
$(\frac{1}{8}\pi r^2) \bar{y} = (\frac{1}{4}\pi r^2) \left( \dfrac{4r}{3\pi} \right) - (\frac{1}{8}\pi r^2)(\frac{1}{2}r)$
$(\frac{1}{8}\pi r^2) \bar{y} = \frac{1}{3}r^3 - \frac{1}{16}\pi r^3$
$(\frac{1}{8}\pi r^2) \bar{y} = 0.137r^3$
$\bar{y} = 0.3488r$ answer
