Problem 532 | Friction
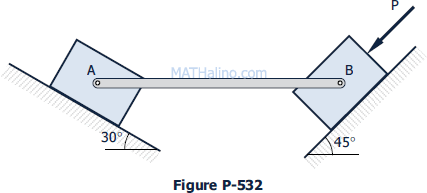
Problem 532
In Fig. P-532, two blocks each weighing 1.5 kN are connected by a uniform horizontal bar which weighs 1.0 kN. If the angle of friction is 15° under each block, find P directed parallel to the 45° incline that will cause impending motion to the left.
- Read more about Problem 532 | Friction
- Log in or register to post comments





Recent comments