Coefficient of friction
$\mu = \tan \phi$
$\mu = \tan 15^\circ$
Amount of friction at contact surfaces
$f_A = \mu N_A = N_A \tan 15^\circ$
$f_B = \mu N_B = N_B \tan 15^\circ$
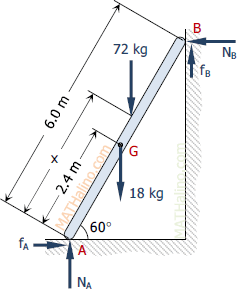
$\Sigma F_V = 0$
$N_A + f_B = 18 + 72$
$N_A = 90 - f_B$
$N_A = 90 - N_B \tan 15^\circ$
$\Sigma F_H = 0$
$f_A = N_B$
$N_A \tan 15^\circ = N_B$
$(90 - N_B \tan 15^\circ) \tan 15^\circ = N_B$
$90 \tan 15^\circ - N_B \tan^2 15^\circ = N_B$
$90 \tan 15^\circ = N_B + N_B \tan^2 15^\circ$
$N_B(1 + \tan^2 15^\circ) = 90 \tan 15^\circ$
$N_B = \dfrac{90 \tan 15^\circ}{1 + \tan^2 15^\circ}$
$N_B = 22.5 \, \text{ kg}$
$f_B = 22.5 \tan 15^\circ$
$f_B = 6.03 \, \text{ kg}$
$\Sigma M_A = 0$
$N_B (6 \sin 60^\circ) + f_B (6 \cos 60^\circ) = 18 (2.4 \cos 60^\circ) + 72(x \cos 60^\circ)$
$N_B (6 \tan 60^\circ) + 6f_B = 18(2.4) + 72x$
$6(22.5) \tan 60^\circ + 6(6.03) = 43.2 + 72x$
$72x = 226.81$
$x = 3.15 \, \text{ m}$ answer
