Problem 519 | Friction

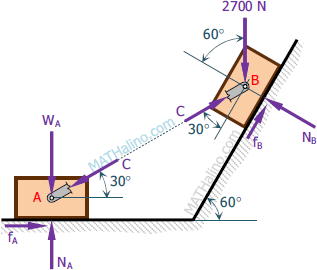
Sum up forces normal to the incline in block B
$N_B = 2700 \cos 60^\circ + C \sin 30^\circ$

$N_B = 1350 + 0.5C$
 

Amount of friction for impending motion of block B
$f_B = \mu N_B = 0.25(1350 + 0.5C)$

$f_B = 337.5 + 0.125C$
 

Sum up all forces parallel to the incline in block B
$f_B + C \cos 30^\circ = 2700 \sin 60^\circ$

$(337.5 + 0.125C) + C \cos 30^\circ = 2700 \sin 60^\circ$

$0.991C = 2000.77$

$C = 2018.89 \, \text{ N}$
 

Summation of vertical forces acting on block A
$N_A = W_A + C \sin 30^\circ$

$N_A = W_A + 2018.89 \sin 30^\circ$

$N_A = W_A + 1009.44$
 

Amount of friction under block A at impending motion
$f_A = \mu N_A = 0.25(W_A + 1009.44)$

$f_A = 0.25W_A + 252.36$
 

Summation of horizontal forces on block A
$f_A = C \cos 30^\circ$

$0.25W_A + 252.36 = 2018.89 \cos 30^\circ$

$W_A = 5984.20 \, \text{ N}$           answer

$\tan \phi = \mu$

$\tan \phi = 0.25$

$\phi = 14.04^\circ$
 

 

$60^\circ - \phi = 45.96^\circ$

$60^\circ + \phi = 74.04^\circ$
 

Apply Sine law to force polygon B
$\dfrac{C}{\sin (60^\circ - \phi)} = \dfrac{2700}{\sin (60^\circ + \phi)}$

$\dfrac{C}{\sin 45.96^\circ} = \dfrac{2700}{\sin 74.04^\circ}$

$C = 2018.72 \, \text{ N}$
 

Sine law to force triangle A
$\dfrac{W_A}{\sin (60^\circ - \phi)} = \dfrac{C}{\sin \phi}$

$\dfrac{W_A}{\sin 45.96^\circ} = \dfrac{2018.72}{\sin 14.04^\circ}$

$W_A = 5981.75 \, \text{ N}$           answer